Question

8．如图，在△ABC中，点D、E分别是AC、AB上的点，AC=7，∠EDC=60°，∠ABC=120°，AE=BC，sinA=$\frac{3\sqrt{3}}{14}$，则四边形DEBC的面积为$\frac{150\sqrt{3}}{49}$．

Answer 1

分析 根据题意做出合适的辅助线，然后根据锐角三角函数和勾股定理可以求得CF、BF、AB的长，然后根据三角形相似可以解答本题．

解答 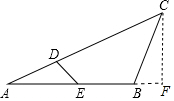解：作CF⊥AB交AB的延长线于点F，如右图所示，
∵AC=7，∠CFA=90°，sinA=$\frac{3\sqrt{3}}{14}$，
∴CF=AC•sinA=$\frac{3\sqrt{3}}{2}$，
∵∠ABC=120°，AE=BC，
∴∠CBF=60°，
∴BC=$\frac{CF}{sin60°}=\frac{\frac{3\sqrt{3}}{2}}{\frac{\sqrt{3}}{2}}=3$，BF=$\frac{CF}{tan60°}=\frac{\frac{3\sqrt{3}}{2}}{\sqrt{3}}=\frac{3}{2}$，
∴AF=$\sqrt{A{C}^{2}-C{F}^{2}}=\frac{13}{2}$，AE=3，
∴AB=AF-BF=$\frac{13}{2}-\frac{3}{2}=5$，
∴${S}_{△ABC}=\frac{AB•CF}{2}=\frac{5×\frac{3\sqrt{3}}{2}}{2}=\frac{15\sqrt{3}}{4}$，
∵∠CDE=60°，
∴∠ADE=120°，
∴∠ADE=∠ABC，
∵∠DAE=∠BAC，
∴△DAE∽△BAC，
∴$（\frac{AE}{AC}）^{2}=\frac{{S}_{△ADE}}{{S}_{△ABC}}$，
即$（\frac{3}{7}）^{2}=\frac{{S}_{△ADE}}{\frac{15\sqrt{3}}{4}}$，
解得，S_△ADE=$\frac{135\sqrt{3}}{196}$，
∴四边形DEBC的面积为：$\frac{15\sqrt{3}}{4}-\frac{135\sqrt{3}}{196}$=$\frac{150\sqrt{3}}{49}$，
故答案为：$\frac{150\sqrt{3}}{49}$．

点评 本题考查解直角三角形，解题的关键是明确题意，作出合适的辅助线，利用锐角三角函数和三角形相似解答．