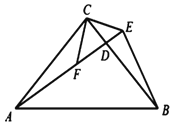
【题目】如图，已知
，
，
，且
、
、
三点共线，
与
交于点
．
（1）求证：
；
（2）若
，
，则 ．
【答案】（1）见详解（2）2
【解析】
(1)如图1中，欲证明
需先证明AF=BE，只要证明△ACF≌△BCE即可.
(2)如图1中，由△ACF≌△BCE，推出∠AFC=∠CEB,由∠CFE=∠CEF=45°，推出∠AFC=∠CEB=135°推出∠AEB=90°，由AC=BC=
，推出BC=
AC=
,在Rt△AEB中，AE=
推出EF=2，由此即可解决问题.
证明:如图中,∵∠ACB=∠FCE=90°∴∠ACF=∠BCE
在△ACF和BCE中,
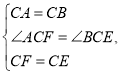
∴△ACF≌△BCE(SAS).
∴ AF=BE,
∴∠CAF=∠CBE,
∵∠CAE+∠EAB+∠ABC=90°
∴∠EAB+∠ABC+∠CBE=90°
∴∠AEB=90
在Rt△AEB中，
BE+AE=AB
∴AF+AE=AB,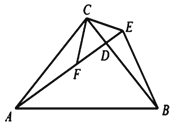
(2) ∵△ACF≌△BCE
∴∠AFC=∠CEB
∵
，
∵∠CFE=∠CEF=45°
∴∠AFC=∠CEB=135°,
∴∠AEB=90°,
∵AC=BC=
∴BC=AC=,
∵BE=3 =AF
在Rt△AEB中，AE=
∴EF=2
故答案为:2
口算题卡加应用题集训系列答案科目：初中数学 来源： 题型：
【题目】已知关于x的一元二次方程
，
（1）求证：该一元二次方程总有两个实数根；
（2）若该方程只有一个小于4的根，求m的取值范围；
（3）若x1，x2为方程的两个根，且n＝x12+x22﹣4，判断动点
所形成的数图象是否经过点
，并说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】在一个不透明的盒子里有5个小球，分别标有数字﹣3，﹣2，﹣1，﹣
，﹣
，这些小球除所标的数不同外其余都相同，先从盒子随机摸出1个球，记下所标的数，再从剩下的球中随机摸出1个球，记下所标的数．
（1）用画树状图或列表的方法求两次摸出的球所标的数之积不大于1的概率．
（2）若以第一次摸出球上的数字为横坐标，第二次摸出球上的数字为纵坐标确定一点，直接写出该点在双曲线y=
上的概率．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图是由边长为1的小正方形组成的方格图．
（1）请在方格图中建立平面直角坐标系，使点
的坐标为(3，3)，点
的坐标为(1，0)；
（2）点
的坐标为(4，1)，在图中找到点，顺次连接点、、，并作出
关于
轴对称的图形
；
（3）中边
边上的高为 ．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】某商品的进价为每件50元．当售价为每件70元时，每星期可卖出300件，现需降价处理，且经市场调查：每降价1元，每星期可多卖出20件．在确保盈利的前提下，解答下列问题：
（1）若设每件降价x元、每星期售出商品的利润为y元，请写出y与x的函数关系式，并求出自变量x的取值范围；
（2）当降价多少元时，每星期的利润最大？最大利润是多少？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在边长为1个单位长度的小正方形组成的网格中，
的顶点均在格点上，点A的坐标为
，点B的坐标为
，点C的坐标为
.
（1）以点C为旋转中心，将旋转
后得到
，请画出；
（2）平移，使点A的对应点
的坐标为
，请画出
;
（3）若将绕点P旋转可得到，则点P的坐标为___________.
查看答案和解析>>
科目：初中数学 来源： 题型：
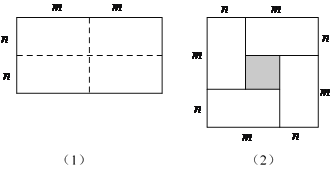
【题目】如图(1)是一个长为2m，宽为2n的长方形，沿图中虚线剪成四个均匀的小长方形，然后按图(2)形状拼成一个正方形.
(1)你认为图(2)中的阴影部分的正方形的边长等于多少？
(2)观察图(2)，你能写出下列三个代数式之间的等量关系吗？代数式：
，
，
；
(3)已知：
，
，求的值.
查看答案和解析>>
科目：初中数学 来源： 题型：
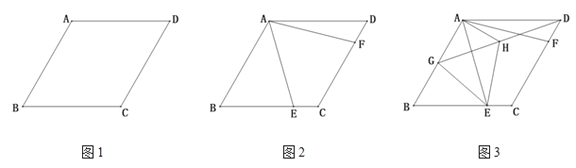
【题目】如图，在菱形ABCD中，∠ABC+∠ADC=120°，将一透明三角板60°角的顶点落在点A上，并绕着点A旋转，三角板的两边分别交BC、CD于点E、F．
（1）如图1，求∠BAD的度数；
（2）如图2，求证：BE+DF=AB；
（3）如图3，在（2）的条件下，取AB中点G，作等边△EGH，连接AH，延长GH刚好与平行四边形ABCD交于点D，若AH⊥AB，△EGH的面积为
．求DH的长．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
