
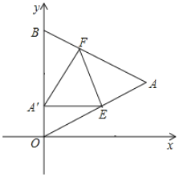
【题目】如图,已知等边![]() 的边长为
的边长为![]() ,顶点
,顶点![]() 在
在![]() 轴正半轴上,将
轴正半轴上,将![]() 折叠,使点
折叠,使点![]() 落在
落在![]() 轴上的点
轴上的点![]() 处,折痕为
处,折痕为![]() .当
.当![]() 是直角三角形时,点
是直角三角形时,点![]() 的坐标为__________.
的坐标为__________.
【答案】![]() ,
,![]()
【解析】
当A′E∥x轴时,△A′EO是直角三角形,可根据∠A′OE的度数用O′A表示出OE和A′E,由于A′E=AE,且A′E+OE=OA=![]() ,由此可求出OA′的长,也就能求出A′E的长,据此可求出A′的坐标;当∠A’EO=90°时,△A′EO是直角三角形,设OE=x,则AE=A’E=
,由此可求出OA′的长,也就能求出A′E的长,据此可求出A′的坐标;当∠A’EO=90°时,△A′EO是直角三角形,设OE=x,则AE=A’E=![]() -x,根据三角函数的关系列出方程即可求解x,从而求出A’的坐标.
-x,根据三角函数的关系列出方程即可求解x,从而求出A’的坐标.
当A′E∥x轴时,△OA′E是直角三角形,
故∠A′OE=60°,A′E=AE,
设A′的坐标为(0,b),
∴AE=A′E=A’Otan60°=![]() b,OE=2b,
b,OE=2b,
![]() b+2b=2+
b+2b=2+![]() ,
,
∴b=1,A′的坐标是(0,1);
当∠A’EO=90°时,△A′EO是直角三角形,
设OE=x,则AE=A’E=![]() -x,
-x,
∵∠AOB=60°,∴A’E=OEtan60°=![]() x=
x=![]() -x
-x
解得x=![]()
∴A’O=2OE=![]()
∴A’(0,![]() )
)
综上,A’的坐标为![]() ,
,![]() .
.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
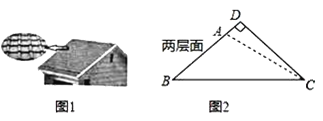
【题目】太阳能光伏建筑是现代绿色环保建筑之一,老张准备把自家屋顶改建成光伏瓦面,改建前屋顶截面△ABC如图2所示,BC=10米,∠ABC=∠ACB=36°,改建后顶点D在BA的延长线上,且∠BDC=90°,求改建后南屋面边沿增加部分AD的长.(结果精确到0.1米)
(参考数据:sin18°≈0.31,cos18°≈0.95.tan18°≈0.32,sin36°≈0.59.cos36°≈0.81,tan36°≈0.73)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在⊿OAB中,∠OAB=90°.OA=AB=6.将⊿OAB绕点O逆时针方向旋转90°得到⊿OA1B1

(1)线段A1B1的长是 ∠AOA1的度数是
(2)连结AA1,求证:四边形OAA1B1是平行四边形 ;
(3)求四边形OAA1B1的面积 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司研发了一款成本为50元的新型玩具,投放市场进行试销售.其销售单价不低于成本,按照物价部门规定,销售利润率不高于90%,市场调研发现,在一段时间内,每天销售数量y(个)与销售单价x(元)符合一次函数关系,如图所示:
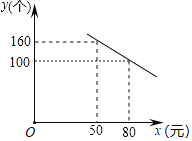
(1)根据图象,直接写出y与x的函数关系式;
(2)该公司要想每天获得3000元的销售利润,销售单价应定为多少元
(3)销售单价为多少元时,每天获得的利润最大,最大利润是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
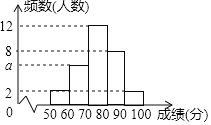
【题目】为了解某次“小学生书法比赛”的成绩情况,随机抽取了30名学生的成绩进行统计,并将统计情况绘成如图所示的频数分布直方图,己知成绩x(单位:分)均满足“50≤x<100”.根据图中信息回答下列问题:
(1)图中a的值为 ;
(2)若要绘制该样本的扇形统计图,则成绩x在“70≤x<80”所对应扇形的圆心角度数为 度;
(3)此次比赛共有300名学生参加,若将“x≥80”的成绩记为“优秀”,则获得“优秀“的学生大约有 人:
(4)在这些抽查的样本中,小明的成绩为92分,若从成绩在“50≤x<60”和“90≤x<100”的学生中任选2人,请用列表或画树状图的方法,求小明被选中的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
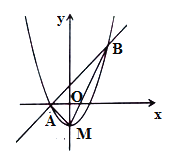
【题目】如图,抛物线![]() 的顶点为
的顶点为![]() ,且抛物线与直线
,且抛物线与直线![]() 相交于
相交于![]() 两点,且点
两点,且点![]() 在
在![]() 轴上,点
轴上,点![]() 的坐标为
的坐标为![]() ,连接
,连接![]() .
.
(1)![]() ,
,![]() ,
,![]() (直接写出结果);
(直接写出结果);
(2)当![]() 时,则
时,则![]() 的取值范围为 (直接写出结果);
的取值范围为 (直接写出结果);
(3)在直线![]() 下方的抛物线上是否存在一点
下方的抛物线上是否存在一点![]() ,使得
,使得![]() 的面积最大?若存在,求出
的面积最大?若存在,求出![]() 的最大面积及点
的最大面积及点![]() 坐标.
坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB为⊙O的直径,AC、DC为弦,∠ACD=60°,P为AB延长线上的点,∠APD=30°.
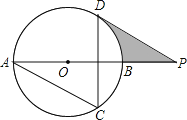
(1)求证:DP是⊙O的切线;
(2)若⊙O的半径为3cm,求图中阴影部分的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
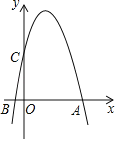
【题目】如图,抛物线y=ax2+bx+6与x轴交于点A(6,0),B(﹣1,0),与y轴交于点C.
(1)求抛物线的解析式;
(2)若点M为该抛物线对称轴上一点,当CM+BM最小时,求点M的坐标.
(3)抛物线上是否存在点P,使△BCP为等腰三角形?若存在,有几个?并请在图中画出所有符合条件的点P,(保留作图痕迹);若不存在,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com