
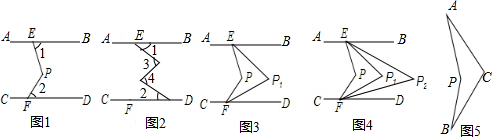
分析 (1)过点P作PH∥AB∥CD,根据平行线的性质:两直线平行,内错角相等即可证得;
(2)同理依据两直线平行,内错角相等即可证得∠1+∠4=∠2+∠3,求得∠4=80°;
(3)利用(1)的结论和角平分线的性质即可写出结论;
(4)过A、B分别作直线AE、BF,使AE∥BF,利用(1)的结论即可求解.
解答 解:(1)如图1,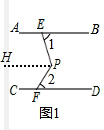
过点P作PH∥AB∥CD
∴∠1=∠EPH,∠2=∠FPH
而∠EPF=∠EPH+∠FPH
∴∠EPF=∠1+∠2=110°;
(2)∠4=80°,(3)∠P1=$\frac{1}{2}$(x+y)°(用x,y的代数式表示)
∠Pn=($\frac{1}{2}$)n(x+y)°.
(4)∠APB=∠C+60°.理由如下:
过A、B分别作直线AE、BF,使AE∥BF.如图,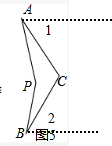
由(1)规律可知∠C=∠1+∠2.
∠APB=∠PAE+∠PBF
=(∠PAC+∠1)+(∠PBC+∠2)
=∠PAC+∠PBC+(∠1+∠2)
=∠C+60°.
点评 本题考查了平行线性质的应用,关键是正确作辅助线,利用性质解决问题.


 一线名师权威作业本系列答案
一线名师权威作业本系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 3.06×104 | B. | 0.3066×105 | C. | 3.066×104 | D. | 3.07×104 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com