
【题目】已知a,b,c满足a+c=b,4a+c=-2b,抛物线y=ax+bx+c(a>0)过点A(-![]() ,y1),B(
,y1),B(![]() ,y2,)C(3,y3),则y1,y2,y3的大小关系为( )
,y2,)C(3,y3),则y1,y2,y3的大小关系为( )
A. y2<y1<y3B. y3<y1<y2C. y2<y3<y1D. y1<y2<y3
【答案】D
【解析】
由a+c=b,4a+c=-2b,可知x=-1时,y=0;x=2时,y=0,从而可知抛物线与x轴的交点坐标,即可得出对称轴为直线x=![]() ,进而可得A点关于直线x=
,进而可得A点关于直线x=![]() 的对称点的坐标,根据a>0,可知抛物线开口向上, 利用二次函数的性质即可得答案.
的对称点的坐标,根据a>0,可知抛物线开口向上, 利用二次函数的性质即可得答案.
∵a+c=b,4a+c=-2b,
∴a-b+c=0,4a+2b+c=0,
∴x=-1时,y=0,x=2时,y=0,即抛物线与x轴的交点为(-1,0)和(2,0),
∴对称轴为直线x=![]() =
=![]() ,
,
∴A(-![]() ,y1)关于直线x=
,y1)关于直线x=![]() 的对称点为(
的对称点为(![]() ,y1),
,y1),
∵a>0,
∴抛物线的开口向上,
∴当x>![]() 时,y随x的增大而增大,
时,y随x的增大而增大,
∵![]() <
<![]() <3,
<3,
∴y1<y2<y3
故选D.


科目:初中数学 来源: 题型:
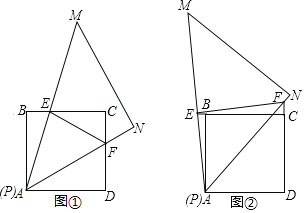
【题目】小明与同学们在数学动手实践操作活动中,将锐角为![]() 的直角三角板MPN的一个锐角顶点P与正方形ABCD的顶点A重合,正方形ABCD固定不动,然后将三角板绕着点A旋转,
的直角三角板MPN的一个锐角顶点P与正方形ABCD的顶点A重合,正方形ABCD固定不动,然后将三角板绕着点A旋转,![]() 的两边分别与正方形的边BC、DC或其延长线相交于点E、F,连结EF.
的两边分别与正方形的边BC、DC或其延长线相交于点E、F,连结EF.
(探究发现)
![]() 在三角板旋转过程中,当
在三角板旋转过程中,当![]() 的两边分别与正方形的边CB、DC相交时,如图
的两边分别与正方形的边CB、DC相交时,如图![]() 所示,请直接写出线段BE、DF、EF满足的数量关系:______.
所示,请直接写出线段BE、DF、EF满足的数量关系:______.
(拓展思考)
![]() 在三角板旋转过程中,当
在三角板旋转过程中,当![]() 的两边分别与正方形的边CB、DC的延长线相交时,如图
的两边分别与正方形的边CB、DC的延长线相交时,如图![]() 所示,则线段BE、DF、EF又将满足怎样的数量关系:______,并证明你的结论;
所示,则线段BE、DF、EF又将满足怎样的数量关系:______,并证明你的结论;
(创新应用)
![]() 若正方形的边长为4,在三角板旋转过程中,当
若正方形的边长为4,在三角板旋转过程中,当![]() 的一边恰好经过BC边的中点时,试求线段EF的长.
的一边恰好经过BC边的中点时,试求线段EF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
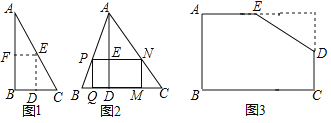
【题目】(探索发现)
![]() 如图1,是一张直角三角形纸片,
如图1,是一张直角三角形纸片,![]() ,小明想从中剪出一个以
,小明想从中剪出一个以![]() 为内角且面积最大的矩形,经过多次操作发现,当沿着中位线DE、EF剪下时,所得的矩形的面积最大,随后,他通过证明验证了其正确性,并得出:矩形的最大面积与原三角形面积的比值为______.
为内角且面积最大的矩形,经过多次操作发现,当沿着中位线DE、EF剪下时,所得的矩形的面积最大,随后,他通过证明验证了其正确性,并得出:矩形的最大面积与原三角形面积的比值为______.
(拓展应用)
![]() 如图2,在
如图2,在![]() 中,
中,![]() ,BC边上的高
,BC边上的高![]() ,矩形PQMN的顶点P、N分别在边AB、AC上,顶点Q、M在边BC上,求出矩形PQMN面积的最大值
,矩形PQMN的顶点P、N分别在边AB、AC上,顶点Q、M在边BC上,求出矩形PQMN面积的最大值![]() 用含a、h的代数式表示
用含a、h的代数式表示![]() ;
;
(灵活应用)
![]() 如图3,有一块“缺角矩形”ABCDE,
如图3,有一块“缺角矩形”ABCDE,![]() ,
,![]() ,
,![]() ,
,![]() ,小明从中剪出了一个面积最大的矩形
,小明从中剪出了一个面积最大的矩形![]() 为所剪出矩形的内角
为所剪出矩形的内角![]() ,直接写出该矩形的面积.
,直接写出该矩形的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】央视“经典咏流传”开播以来受到社会广泛关注,某校就“中华文化我传承——地方戏曲进校园”的喜爱情况进行了随机调查,对收集的信息进行统计,绘制了下面两幅统计图:
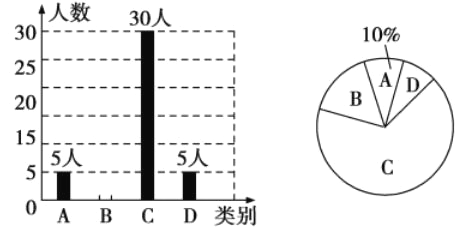
请你根据统计图所提供的信息解答下列问题:
本次调查的总人数为_____,扇形统计图中C类所在扇形的圆心角度数为_____;
(2)补全条形统计图;
(3)若该校共有学生1800人,请根据上述调查结果,估计该校学生中A类有 人;
(4)在抽取的A类5人中,刚好有3名女生2名男生,从中随机抽取两个同学担任两角色,用画树状图法或列表法求出被抽到的两名学生性别相同的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
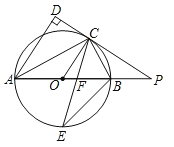
【题目】如图,已知![]() 是圆
是圆![]() 的直径,点
的直径,点![]() 是圆
是圆![]() 上一点,
上一点,![]() 与过点
与过点![]() 的切线垂直,垂足为点
的切线垂直,垂足为点![]() ,直线
,直线![]() 与
与![]() 的延长线相交于点
的延长线相交于点![]() ,弦
,弦![]() 平分
平分![]() ,交
,交![]() 于点
于点![]() ,连接
,连接![]()
(1)求证:![]() 平分
平分![]() ;
;
(2)求证:![]() 是等腰三角形;
是等腰三角形;
(3)若![]() ,
,![]() ,求圆
,求圆![]() 的半径长.
的半径长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两家草莓采摘园的草莓品质相同,销售价格也相同.“五一期间”,两家均推出了优惠方案,甲采摘园的优惠方案是:游客进园需购买50元的门票,采摘的草莓六折优惠;乙采摘园的优惠方案是:游客进园不需购买门票,采摘园的草莓超过一定数量后,超过部分打折优惠.优惠期间,设某游客的草莓采摘量为x(千克),在甲采摘园所需总费用为![]() (元),在乙采摘园所需总费用为
(元),在乙采摘园所需总费用为![]() (元),图中折线OAB表示
(元),图中折线OAB表示![]() 与x之间的函数关系.
与x之间的函数关系.

(1)甲、乙两采摘园优惠前的草莓销售价格是每千克 元;
(2)求![]() 、
、![]() 与x的函数表达式;
与x的函数表达式;
(3)在图中画出![]() 与x的函数图象,并写出选择甲采摘园所需总费用较少时,草莓采摘量x的范围.
与x的函数图象,并写出选择甲采摘园所需总费用较少时,草莓采摘量x的范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,反比例函数y=![]() (k>0)的图象与半径为5的⊙O交于M、N两点,△MON的面积为3.5,若动点P在x轴上,则PM+PN的最小值是_____.
(k>0)的图象与半径为5的⊙O交于M、N两点,△MON的面积为3.5,若动点P在x轴上,则PM+PN的最小值是_____.
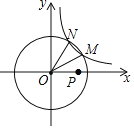
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某小区有一块长为30m,宽为24m的矩形空地,计划在其中修建两块相同的矩形绿地,它们的面积之和为480m2,两块绿地之间及周边有宽度相等的人行通道,设人行通道的宽度为xm,则可列方程为_____.
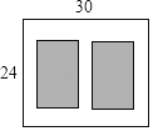
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某人在山坡坡脚C处测得一座建筑物顶点A的仰角为63.4°,沿山坡向上走到P处再测得该建筑物顶点A的仰角为53°.已知BC=90米,且B、C、D在同一条直线上,山坡坡度i=5:12.
(1)求此人所在位置点P的铅直高度.(结果精确到0.1米)
(2)求此人从所在位置点P走到建筑物底部B点的路程(结果精确到0.1米)
(测倾器的高度忽略不计,参考数据:tan53°≈![]() ,tan63.5°≈2)
,tan63.5°≈2)

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com