
分析 (1)根据市场价为每千克30元,以后每千克活蟹的市场价每天可上升1元,可列出P关于x的函数关系式;
(2)根据销售额Q=活蟹的销售额+死蟹的销售额,列出Q于x的函数关系式;
(3)根据利润=销售总额-收购成本-费用,列出利润与x天的函数关系,运用函数性质求出最值即可.
解答 解:(1)由题意知:p=30+x;
(2)由题意知:
活蟹的销售额为(1000-10x)(30+x)元,
死蟹的销售额为200x元,
∴Q=(1000-10x)(30+x)+200x=-10x2+900x+30000;
(3)设总利润为L=Q-30000-400x=-10x2+500x,
=-10(x2-50x)=-10(x2-50x+252-252)=-10(x-25)2+6250.
当x=25时,总利润最大,最大利润为6250元.
点评 此题主要考查了二次函数的应用以及二次函数最值求法,理解题意列出函数关系式是解题关键.


科目:初中数学 来源: 题型:选择题
| A. | 射击运动员只射击1次,就命中靶心 | |
| B. | 任取一个实数x,都有|x|≥0 | |
| C. | 画一个三角形,使其三边的长分别为8cm,6cm,2cm | |
| D. | 抛掷一枚质地均匀且六个面分别刻有1到6的点数的正方体骰子,朝上一面的点数为6 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
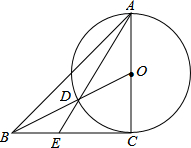 一等腰三角形ABC,AC边的中点O为圆心,以AO为半径作圆,连接BO与O交于点D,延长AD交BC于点E,已知BD=CE,求证:BC为切线.
一等腰三角形ABC,AC边的中点O为圆心,以AO为半径作圆,连接BO与O交于点D,延长AD交BC于点E,已知BD=CE,求证:BC为切线.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com