
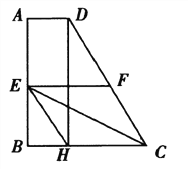
【题目】如图,在四边形ABCD中,AD∥BC,AB⊥BC,AD=2,BC=6,CD=8,E,F分别是边ABCD的中点, DH⊥BC于点H,连接EH,EC,EF,现有下列结论:①∠CDH=30°;②EF=4;③四边形EFCH是菱形;④S△EFC=3S△BEH.你认为结论正确的有___________.(填序号)
 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案科目:初中数学 来源: 题型:
【题目】如图(1),在Rt△ABC中,∠A=90°,AC=AB=4,D,E分别是AB,AC的中点.若等腰Rt△ADE绕点A逆时针旋转,得到等腰Rt△AD1E1,如图(2),设旋转角为α(0<α≤180°),记直线BD1与CE1的交点为P.
(1)求证:BD1=CE1;(2)当∠CPD1=2∠CAD1时,求CE1的长;
(3)连接PA,△PAB面积的最大值为 .(直接填写结果)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某饮料厂开发了A、B两种新型饮料,主要原料均为甲和乙,每瓶饮料中甲、乙的含量如下表所示.现用甲原料和乙原料各2800克进行试生产,计划生产A、B两种饮料共100瓶.设生产A种饮料x瓶,解析下列问题:
原料名称 饮料名称 | 甲 | 乙 |
A | 20克 | 40克 |
B | 30克 | 20克 |
(1)有几种符合题意的生产方案写出解析过程;
(2)如果A种饮料每瓶的成本为2.60元,B种饮料每瓶的成本为2.80元,这两种饮料成本总额为y元,请写出y与x之间的关系式,并说明x取何值会使成本总额最低?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】大家看过中央电视台“购物街”节目吗?其中有一个游戏环节是大转轮比赛,转轮上平均分布着5、10、15、20一直到100共20个数字.选手依次转动转轮,每个人最多有两次机会.选手转动的数字之和最大不超过100者为胜出;若超过100则成绩无效,称为“爆掉”.
(1)某选手第一次转到了数字5,再转第二次,则他两次数字之和为100的可能性有多大?
(2)现在某选手第一次转到了数字65,若再转第二次了则有可能“爆掉”,请你分析“爆掉”的可能性有多大?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了节省材料,某水产养殖户利用水库的岸堤为一边,用总长为![]() 米(
米(![]() 为大于
为大于![]() 的常数)的围网在水库中围成了如图所示的①②两块矩形区域.已知岸堤的可用长度不超过
的常数)的围网在水库中围成了如图所示的①②两块矩形区域.已知岸堤的可用长度不超过![]() 米.设
米.设![]() 的长为
的长为![]() 米,矩形区域
米,矩形区域![]() 的面积为
的面积为![]() 平方米
平方米
(1)求![]() 与
与![]() 之间的函数关系,并直接写出自变量
之间的函数关系,并直接写出自变量![]() 的取值范围(用含
的取值范围(用含![]() 的式子表示).
的式子表示).
(2)若![]() ,求
,求![]() 的最大值,并求出此时
的最大值,并求出此时![]() 的值.
的值.
(3)若![]() ,请求出
,请求出![]() 的最大值.
的最大值.

查看答案和解析>>
科目:初中数学 来源: 题型:
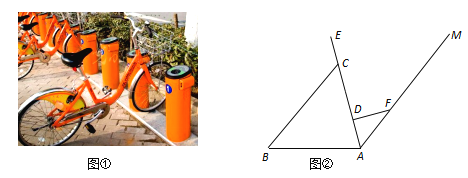
【题目】“低碳环保,你我同行”.近几年,各大城市的公共自行车给市民出行带来了极大的方便.图①是公共自行车的实物图,图②是公共自行车的车架示意图,点A.D、C、E在同一条直线上,CD=30cm,DF=20cm,AF=25cm,FD⊥AE于点D,座杆CE=15cm,且∠EAB=75°.
(1)求AD的长;
(2)求点E到AB的距离.(参考数据:sin75°≈0.97,cos75°≈0.26,tan75°≈3.73)
查看答案和解析>>
科目:初中数学 来源: 题型:
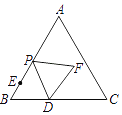
【题目】如图,在等边△ABC中,AB=10,BD=4,BE=2,点P从点E出发沿EA方向运动,连结PD,以PD为边,在PD的右侧按如图所示的方式作等边△DPF,当点P从点E运动到点A时,点F运动的路径长是________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在梯形ABCD中,∠A=∠B=90°,AB=![]() ,点E在AB上,∠AED=45°,DE=6,CE=7.
,点E在AB上,∠AED=45°,DE=6,CE=7.
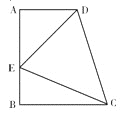
(1)求AE的长;
(2)求sin∠BCE的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
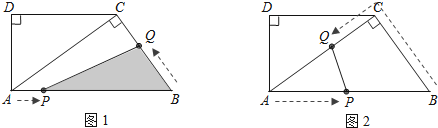
【题目】如图1,DC∥AB,∠D=90°,AC⊥BC,AB=10cm,BC=6cm. 点P以1cm/s的速度从点A出发,沿AB方向向点B运动,同时点Q以2cm/s的速度从点B出发,沿B→C→A方向向点A运动,当一个运动点到达终点时,另一个运动点也随之停止运动,设运动的时间为t(s).
(1)① 求证:△ACD∽△BAC;② 求DC的长;
(2)当点Q在边BC上运动,求t为何值时,△PBQ的面积为![]() cm2;
cm2;
(3)如图2,当点Q在边CA上运动,求t为何值时,PQ∥BC.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com