
【题目】已知,如图,△ABC是等边三角形,AE=CD,BQ⊥AD于Q,BE交AD于点P,下列说法:①∠APE=∠C,② AQ=BQ,③BP=2PQ, ④AE+BD=AB,其正确的个数有( )个.
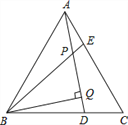
A. 1 B. 2 C. 3 D. 4
【答案】C
【解析】试题解析:∵△ABC是等边三角形,
∴AB=AC,∠BAE=∠C=60°,
在△ABE和△CAD中,
AB=AC,∠BAE=∠C,AE=CD,
∴△ABE≌△CAD(SAS).
∴∠ABE =∠CAD,
∴∠BPQ=∠ABE +∠BAP=∠CAD +∠BAP =∠BAC=60°,
∴∠APE=∠BPQ=60°,
∴∠APE=∠C.
故①结论正确;
∵BQ⊥AD,
∴∠PBQ=90°-∠BPQ=90°-60°=30°,
∴BP=2PQ.
故③结论正确;
∵△ABE≌△CAD,
∴AE=CD,
∴AE+BD=CD+BD=BC=AB.
故④结论正确;
无法证明AQ=BQ成立,故②结论错误.
故选C.


 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案科目:初中数学 来源: 题型:
【题目】国家发改委发布信息,到2019年12月底,高速公路电子不停车快速收费(ETC)用户数量将突破1.8亿,将180 000 000科学记数法表示为____________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某快递员准备送出一批美术用纸共25500包,其中包括素描纸、手工彩色卡纸和水粉纸三种美术用纸,它们的数量比为1:2:14.该快递员准备送出的这三种美术用纸各多少包?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2015年茂名市生产总值约2450亿元,将2450用科学记数法表示为( )
A.0.245×104
B.2.45×103
C.24.5×102
D.2.45×1011
查看答案和解析>>
科目:初中数学 来源: 题型:
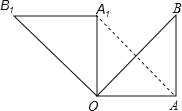
【题目】如图,在Rt△OAB中,∠OAB=90°,OA=AB=6,将△OAB绕点O沿逆时针方向旋转90°得到△OA1B1.
(1)线段OA1的长是 ,∠AOB1的度数是 ;
(2)连接AA1,求证:四边形OAA1B1是平行四边形;
(3)求点B旋转到点B1的位置所经过的路线的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某一项工程,在工程招标时,接到甲、乙两个工程队的投标书,施工一天,需付甲工程队工程款1.5万元,乙工程队工程款1.1万元,工程领导小组根据甲乙两队的投标书测算,可有三种施工方案:
(1)甲队单独完成这项工程刚好如期完成;
(2)乙队单独完成这项工程要比规定日期多用5天;
(3)若甲、乙两队合作4天,余下的工程由乙队单独也正好如期完成.
在不耽误工期的情况下,你觉得那一种施工方案最节省工程款?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com