
【题目】在平面直角坐标系中,抛物线y=﹣(x﹣m)2+4(m>0)的顶点为A,与直线x=![]() 相交于点B,点A关于直线x=
相交于点B,点A关于直线x=![]() 的对称点为C.
的对称点为C.
(1)若抛物线y=﹣(x﹣m)2+4(m>0)经过原点,求m的值.
(2)点C的坐标为 .用含m的代数式表示点B到直线AC的距离为 .
(3)将y=﹣(x﹣m)2+4(m>0,且x≥![]() )的函数图象记为图象G,图象G关于直线x=
)的函数图象记为图象G,图象G关于直线x=![]() 的对称图象记为图象H.图象G与图象H组合成的图象记为图象M.
的对称图象记为图象H.图象G与图象H组合成的图象记为图象M.
①当图象M与x轴恰好有三个交点时,求m的值.
②当△ABC为等腰直角三角形时,直接写出图象M所对应的函数值小于0时,自变量x的取值范围.
【答案】(1)m=2.(2)(0,4),![]() ;(3)①m=4,②x<﹣2或x>4.
;(3)①m=4,②x<﹣2或x>4.
【解析】
(1)将原点坐标代入解出即可.
(2)根据顶点公式算出C点坐标即可,算出AC的解析式,再求出B到AC的距离.
(3)①画出图象即可看出B的坐标,列式计算即可;②分别表示出A、B、C的坐标,令BE=AE代入算出结果.
(1)∵抛物线y=﹣(x﹣m)2+4(m>0)经过原点,
∴0=﹣(0﹣m)2+4,
解得 m1=2,m2=﹣2,
∵m>0,
∴m=2.
(2)∵抛物线y=﹣(x﹣m)2+4(m>0),
∴顶点A坐标为(m,4),
∵点A关于直线x=![]() 的对称点为C.
的对称点为C.
∴点C的坐标为(0,4);
∴直线AC解析式为y=4,
当x=![]() 时,y=﹣
时,y=﹣![]() +4,
+4,
∴点B(![]() ,﹣
,﹣![]() +4),
+4),
∴点B到直线AC的距离为![]() ,
,
故答案为:(0,4),![]() ;
;
(3)①如图,当图象M与x轴恰好有三个交点时,
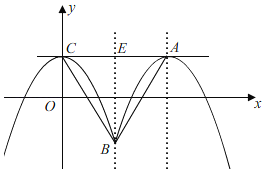
∴点 B在x轴上,且点B(![]() ,﹣
,﹣![]() +4),
+4),
∴0=﹣![]() +4
+4
∴m1=4,m2=﹣4(舍去)
②∵△ABC为等腰直角三角形,
∴BE=CE=AE=![]() AC,
AC,
∵B(![]() ,﹣
,﹣![]() +4),A(m,2),C(0,2),(m>0)
+4),A(m,2),C(0,2),(m>0)
∴BE=![]() ,AE=|
,AE=|![]() |=
|=![]() ,
,
∴![]() =
=![]()
∴m1=2,m2=0(不合题意舍去),
∴抛物线解析式为:y=﹣(x﹣2)2+4,
当y=0时,0=﹣(x﹣2)2+4,
∴x1=0<![]() =1(不合题意舍去),x2=4,
=1(不合题意舍去),x2=4,
∴图象G与x轴的交点为(4,0),且图象G关于直线x=![]() 的对称图象记为图象H.
的对称图象记为图象H.
∴图象H与x轴的交点为(﹣2,0),
∴图象M与x轴的交点为(﹣2,0)与(4,0),
∵图象M所对应的函数值小于0,
∴x<﹣2或x>4.


 优秀生应用题卡口算天天练系列答案
优秀生应用题卡口算天天练系列答案 浙江之星课时优化作业系列答案
浙江之星课时优化作业系列答案 激活思维优加课堂系列答案
激活思维优加课堂系列答案科目:初中数学 来源: 题型:
【题目】如图,CB=CA,∠ACB=90°,点D在边BC上(与B,C不重合),四边形ADEF为正方形,过点F作FG⊥CA,交CA的延长线于点G,连接FB,交DE于点Q,给出以下结论:①AC=FG;②S△FAB∶S四边形CBFG=1∶2;③∠ABC=∠ABF;④AD2=FQ·AC,其中正确结论的个数是( )
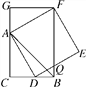
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
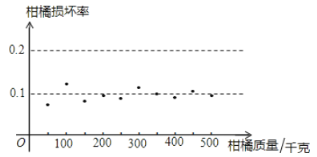
【题目】某水果公司以2元/千克的成本购进10000千克柑橘,销售人员在销售过程中随机抽取柑橘进行“柑橘损坏率”统计,并绘制成如图所示的统计图,根据统计图提供的信息解决下面问题:
(1)柑橘损坏的概率估计值为 ;估计这批柑橘完好的质量为 千克.
(2)若希望这批柑橘能够获得利润5000元,那么在出售柑橘(只卖好果)时,每千克大约定价为多少元比较合适?(精确到0.1)
查看答案和解析>>
科目:初中数学 来源: 题型:
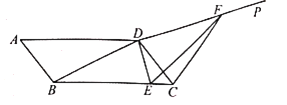
【题目】如图,在![]() 中,
中,![]() ,对角线
,对角线![]() ,点E是线段BC上的动点,连接DE,过点D作DP⊥DE,在射线DP上取点F,使得
,点E是线段BC上的动点,连接DE,过点D作DP⊥DE,在射线DP上取点F,使得![]() ,连接CF,则
,连接CF,则![]() 周长的最小值为___________.
周长的最小值为___________.
查看答案和解析>>
科目:初中数学 来源: 题型:
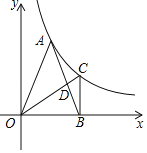
【题目】如图,A为反比例函数y=![]() (其中x>0)图象上的一点,在x轴正半轴上有一点B,OB=4.连接OA、AB,且OA=AB=2
(其中x>0)图象上的一点,在x轴正半轴上有一点B,OB=4.连接OA、AB,且OA=AB=2![]() .
.
(1)求k的值;
(2)过点B作BC⊥OB,交反比例函数y=![]() (x>0)的图象于点C.
(x>0)的图象于点C.
①连接AC,求△ABC的面积;
②在图上连接OC交AB于点D,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】现有A、B两个不透明袋子,分别装有3个除颜色外完全相同的小球.其中,A袋装有2个白球,1个红球;B袋装有2个红球,1个白球.
(1)将A袋摇匀,然后从A袋中随机取出一个小球,则摸出小球是白色的概率为 ;
(2)小华和小林商定了一个游戏规则:从摇匀后的A,B两袋中随机摸出一个小球,摸出的这两个小球,若颜色相同,则小林获胜;若颜色不同,则小华获胜.请用列表或画出树状图的方法说明这个游戏规则对双方是否公平.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,矩形ABCD中,AB=4cm,BC=8cm,AC的垂直平分线EF分别交AD、BC于点E、F,垂足为O.
(1)如图(1),连接AF、CE.
①四边形AFCE是什么特殊四边形?说明理由;
②求AF的长;
(2)如图(2),动点P、Q分别从A、C两点同时出发,沿△AFB和△CDE各边匀速运动一周.即点P自A→F→B→A停止,点Q自C→D→E→C停止.在运动过程中,已知点P的速度为每秒5cm,点Q的速度为每秒4cm,运动时间为t秒,当A、C、P、Q四点为顶点的四边形是平行四边形时,求t的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
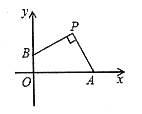
【题目】如图,点![]() 的坐标为
的坐标为![]() ,点
,点![]() ,
,![]() 分别在
分别在![]() 轴,
轴,![]() 轴的正半轴上运动,且
轴的正半轴上运动,且![]() ,下列结论:
,下列结论:
①![]()
②当![]() 时四边形
时四边形![]() 是正方形
是正方形
③四边形![]() 的面积和周长都是定值
的面积和周长都是定值
④连接![]() ,
,![]() ,则
,则![]() ,其中正确的有( )
,其中正确的有( )
A.①②B.①②③C.①②④D.①②③④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com