【题目】已知：数轴上A、B两点表示的有理数分别为a、b，且（a﹣1）2+|b+2|=0，
（1）求（a+b）2015的值．
（2）数轴上的点C与A、B两点的距离的和为7，求点C在数轴上表示的数c的值．
【答案】（1）﹣1；（2）c的值是﹣4或3．见解析
【解析】
试题分析：（1）根据（a﹣1）2+|b+2|=0，可以求得a、b的值，从而可以得到（a+b）2015的值；
（2）由第（1）问中求得的a的值和数轴上的点C与A、B两点的距离的和为7，可知点C可能在点B的左侧或点C可能在点A的右侧两种情况，然后进行计算即可解答本题．
解：（1）∵（a﹣1）2+|b+2|=0，
∴a﹣1=0，b+2=0，
解得a=1，b=﹣2，
∴（a+b）2015=（1﹣2）2015=（﹣1）2015=﹣1；
（2）∵a=1，b=﹣2，数轴上A、B两点表示的有理数分别为a、b，数轴上的点C与A、B两点的距离的和为7，
∴点C可能在点B的左侧或点C可能在点A的右侧，
当点C在点B的左侧时，1﹣c+﹣2﹣c=7，得c=﹣4，
当点C在点A的右侧时，c﹣1+c﹣（﹣2）=7，得c=3，
即点C在数轴上表示的数c的值是﹣4或3．
科目：初中数学 来源： 题型：
【题目】如图，AB是⊙O的直径，过点B作⊙O的切线BM，弦CD∥BM，交AB于点F，且DA=DC，链接AC，AD，延长AD交BM地点E．
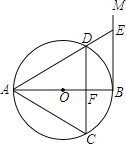
（1）求证：△ACD是等边三角形．
（2）连接OE，若DE=2，求OE的长．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知下列实数：①﹣
，②
，③3.14，④
，⑤0，⑥﹣1.23，⑦
，⑧1.232 232 223…（两个“3”之间依次多一个“2”），⑨﹣
．其中无理数有： ；整数有： ；负分数有： （只需填序号）．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知直线l1：y=﹣
与直线l2：y=kx﹣
交于x轴上的同一个点A，直线l1与y轴交于点B，直线l2与y轴的交点为C．
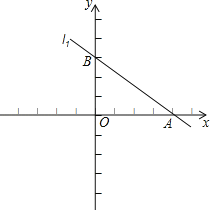
（1）求k的值，并作出直线l2图象；
（2）若点P是线段AB上的点且△ACP的面积为15，求点P的坐标；
（3）若点M、N分别是x轴上、线段AC上的动点（点M不与点O重合），是否存在点M、N，使得△ANM≌△AOC？若存在，请求出N点的坐标；若不存在，请说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】在△ABC中，∠BAC=90°，AB=AC，在△ABC的外部作∠ACM，使得∠ACM=
∠ABC，点D是直线BC上的动点，过点D作直线CM的垂线，垂足为E，交直线AC于F．
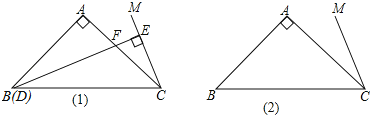
（1）如图1所示，当点D与点B重合时，延长BA，CM交点N，证明：DF=2EC；
（2）当点D在直线BC上运动时，DF和EC是否始终保持上述数量关系呢？请你在图2中画出点D运动到CB延长线上某一点时的图形，并证明此时DF与EC的数量关系．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图所示，在△ABC中，AB=AC，∠A=36°，两条角平分线BE、CD相交于点O，则图中等腰三角形有（ ）
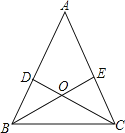
A．3个 B．5个 C．7个 D．8个
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在平面直角坐标系中，点P的坐标为（0，2），直线y=
与x轴、y轴分别交于点A，B，点M是直线AB上的一个动点，则PM长的最小值为（ ）
A．3 B．4 C．5 D．6
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com