
【题目】在△ABC中,∠BAC=90°,AB=AC,在△ABC的外部作∠ACM,使得∠ACM=![]() ∠ABC,点D是直线BC上的动点,过点D作直线CM的垂线,垂足为E,交直线AC于F.
∠ABC,点D是直线BC上的动点,过点D作直线CM的垂线,垂足为E,交直线AC于F.
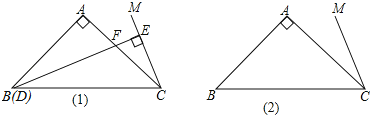
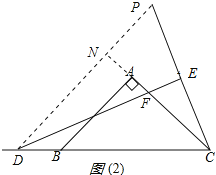
(1)如图1所示,当点D与点B重合时,延长BA,CM交点N,证明:DF=2EC;
(2)当点D在直线BC上运动时,DF和EC是否始终保持上述数量关系呢?请你在图2中画出点D运动到CB延长线上某一点时的图形,并证明此时DF与EC的数量关系.
【答案】(1)见解析;(2)DF=2CE
【解析】
试题分析:(1)延长BA,CM交点N,先证明BC=BN,得出CN=2CE,再证明△BAF≌△CAN,得出对应边相等BF=CN,即可得出结论;
(2)作∠PDE=22.5,交CE的延长线于P点,交CA的延长线于N,先证明PD=CD,得出PC=2CE,再证明△DNF≌△PNC,得出对应边相等DF=PC,即可得出结论.
解:(1)如图(1),延长BA,CM交点N,
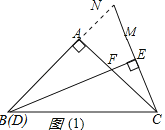
∵∠A=90°,AB=AC,
∴∠ABC=∠ACB=45°,
∵∠ACM=![]() ∠ABC=22.5°,
∠ABC=22.5°,
∴∠BCM=67.5°,
∴∠BNC=67.5°=∠BCM,
∴BC=BN,
∵BE⊥CE,
∴∠ABE=22.5°,CN=2CE,
∴∠ABE=∠ACM=22.5°,
在△BAF和△CAN中,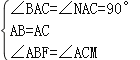 ,
,
∴△BAF≌△CAN(ASA),
∴BF=CN,
∴BF=2CE;
(2)保持上述关系;BF=2CE;
证明如下:
作∠PDE=22.5,交CE的延长线于P点,交CA的延长线于N,
如图(2)所示:
∵DE⊥PC,∠ECD=67.5,
∴∠EDC=22.5°,
∴∠PDE=∠EDC,∠NDC=45°,
∴∠DPC=67.5°,
∴PD=CD,
∴PE=EC,
∴PC=2CE,
∵∠NDC=45°,∠NCD=45°,
∴∠NCD=∠NDC,∠DNC=90°,
∴ND=NC且∠DNC=∠PNC,
在△DNF和△PNC中,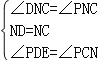 ,
,
∴△DNF≌△PNC(ASA),
∴DF=PC,
∴DF=2CE.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,E,F分别是平行四边形ABCD的边AB,DC上的点,AF与DE相交于点P,FB与EC相交于点B,若S△APD=15cm2,S△BQC=25cm2,则阴影部分的面积为( )
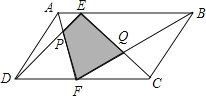
A.10cm2 B.20cm2 C.30cm2 D.40cm2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:数轴上A、B两点表示的有理数分别为a、b,且(a﹣1)2+|b+2|=0,
(1)求(a+b)2015的值.
(2)数轴上的点C与A、B两点的距离的和为7,求点C在数轴上表示的数c的值.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在Rt△ABC中,∠ACB=90°,AC=BC,D为BC中点,CE⊥AD于E,BF∥AC交CE的延长线于F.

(1)求证:△ACD≌△CBF;
(2)求证:AB垂直平分DF.
查看答案和解析>>
科目:初中数学 来源: 题型:
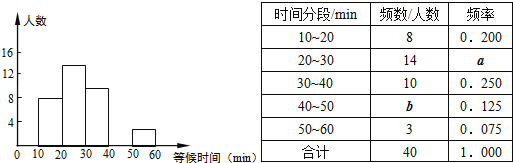
【题目】某公园元旦期间,前往参观的人非常多.这期间某一天某一时段,随机调查了部分入园游客,统计了他们进园前等候检票的时间,并绘制成如下图表.表中“10~20”表示等候检票的时间大于或等于10min而小于20min,其它类同.
(1)这里采用的调查方式是 (填“普查”或“抽样调查”),样本容量是 ;
(2)表中a= ,b= ,并请补全频数分布直方图;
(3)在调查人数里,若将时间分段内的人数绘成扇形统计图,则“40~50”的圆心角的度数是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察下列算式:21=2,22=4,23=8,24=16,25=32,26=64,27=128,28=256,…根据上述算式中的规律,你认为220的末位数字是( )
A.2 B.4 C.6 D.8
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com