
【题目】如图所示,在![]() 中,
中,![]() ,
,![]() ,
,![]() 是
是![]() 的内心,延长
的内心,延长![]() 交
交![]() 的外接圆于点
的外接圆于点![]() ,则
,则![]() 的度数是( )
的度数是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】D
【解析】
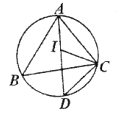
欲求∠ICD的度数,需求∠ICB和∠BCD的度数,由I是内心,可得IC是∠ACB的角平分线,则∠ICB的度数可求;由圆周角定理的推论,同弧或等弧所对的圆周角相等,可得∠BCD=∠BAD,同样的道理,∠BAD是∠BAC的一半;由三角形内角和定理,可求出∠BAC,即可求得∠ICD.
解:∵I是△ABC的内心,
∴AI、CI分别是∠BAC、∠ACB的角平分线.
∵∠ABC=50°,∠ACB=60°,
∴∠BAC=180°-60°-50°=70°,
∴∠BAD=![]() ∠BAC=35°,∠ICB=
∠BAC=35°,∠ICB=![]() ∠ACB=30°.
∠ACB=30°.
∵∠BCD=∠BAD,
∴∠BCD=35°,
∴∠ICD=∠ICB+∠BCD=30°+35°=65°.
故选D.


科目:初中数学 来源: 题型:
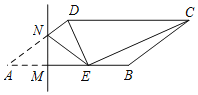
【题目】如图,已知ABCD中,AB=16,AD=10,sinA=![]() ,点M为AB边上一动点,过点M作MN⊥AB,交AD边于点N,将∠A沿直线MN翻折,点A落在线段AB上的点E处,当△CDE为直角三角形时,AM的长为_____.
,点M为AB边上一动点,过点M作MN⊥AB,交AD边于点N,将∠A沿直线MN翻折,点A落在线段AB上的点E处,当△CDE为直角三角形时,AM的长为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
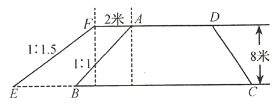
【题目】如图,沿水库拦水坝的背水坡将坝顶加宽2米,坡度由原来的![]() 改为
改为![]() .已知坝高8米,坝长为60米.
.已知坝高8米,坝长为60米.
求:(1)加宽部分横断面![]() 的面积;
的面积;
(2)完成这一工程需要多少立方米土?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,抛物线y=﹣![]() 与x轴交于A、B两点(点A在点B左侧),与y轴交于点C.
与x轴交于A、B两点(点A在点B左侧),与y轴交于点C.
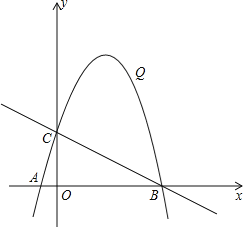
(1)求出△ABC的周长.
(2)在直线BC上方有一点Q,连接QC、QB,当△QBC面积最大时,一动点P从Q出发,沿适当路径到达y轴上的M点,再沿与对称轴垂直的方向到达对称轴上的N点,连接BN,求QM+MN+BN的最小值.
(3)在直线BC上找点G,K是平面内一点,在平面内是否存在点G,使以O、C、G、K为顶点的四边形是菱形?若存在,求出K的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC是等边三角形,以AB为直径作⊙O,交BC边于点D,交AC边于点F,作DE⊥AC于点E.
(1)求证:DE是⊙O的切线;
(2)若△ABC的边长为4,求EF的长度.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,M、N是对角线AC上的两个动点,P是正方形四边上的任意一点,且AB=4,MN=2,设AM=x,在下列关于△PMN是等腰三角形和对应P点个数的说法中,
①当x=0(即M、A两点重合)时,P点有6个;
②当P点有8个时,x=2![]() ﹣2;
﹣2;
③当△PMN是等边三角形时,P点有4个;
④当0<x<4![]() ﹣2时,P点最多有9个.
﹣2时,P点最多有9个.
其中结论正确的是( )

A. ①② B. ①③ C. ②③ D. ③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】文明交流互鉴是推动人类文明进步和世界和平发展的重要动力.2019年5月“亚洲文明对话大会”在北京成功举办,引起了世界人民的极大关注.某市一研究机构为了了解10~60岁年龄段市民对本次大会的关注程度,随机选取了100名年龄在该范围内的市民进行了调查,并将收集到的数据制成了尚不完整的频数分布表、频数分布直方图和扇形统计图,如下所示:
组别 | 年龄段 | 频数(人数) |
第1组 |
| 5 |
第2组 |
|
|
第3组 |
| 35 |
第4组 |
| 20 |
第5组 |
| 15 |
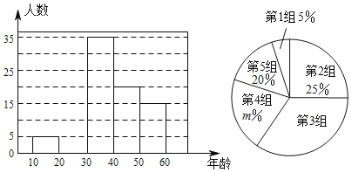
(1)请直接写出![]() ,
,![]() ,第3组人数在扇形统计图中所对应的圆心角是 度.
,第3组人数在扇形统计图中所对应的圆心角是 度.
(2)请补全上面的频数分布直方图;
(3)假设该市现有10~60岁的市民300万人,问40~50岁年龄段的关注本次大会的人数约有多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线经过两点A(﹣3,0),B(0,3),且其对称轴为直线x=﹣1.
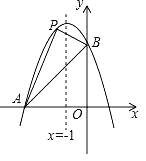
(1)求此抛物线的解析式.
(2)若点Q是对称轴上一动点,当OQ+BQ最小时,求点Q的坐标.
(3)若点P是抛物线上点A与点B之间的动点(不包括点A,点B),求△PAB面积的最大值,并求出此时点P的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com