Question

【题目】如图，已知ABCD中，AB＝16，AD＝10，sinA＝，点M为AB边上一动点，过点M作MN⊥AB，交AD边于点N，将∠A沿直线MN翻折，点A落在线段AB上的点E处，当△CDE为直角三角形时，AM的长为_____．

Answer 1

【答案】4或8﹣

【解析】

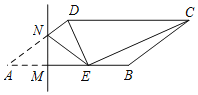
①当∠CDE＝90°，如图1，根据折叠的性质得到MN⊥AB，AM＝EM，得到AN＝DN＝AD＝5，设MN＝3x，AN＝5x＝5，于是得到AM＝4；②当∠DEC＝90°，如图2，过D作DH⊥AB于H，根据相似三角形的性质得到，由sinA＝，AD＝10，得到DH＝6，AH＝8，设HE＝x，根据勾股定理求出x的值，继而求得AE的值，从而得到AM的值，即可得到结论．

当△CDE为直角三角形时，

①当∠CDE＝90°，如图1，

∵在ABCD中，AB∥CD，

∴DE⊥AB，

∵将∠A沿直线MN翻折，点A落在线段AB上的点E处，

∴MN⊥AB，AM＝EM，

∴MN∥DE，

∴AN＝DN＝AD＝5，

∵sinA＝，

∴设MN＝3x，AN＝5x＝5，

∴MN＝3，

∴AM＝4；

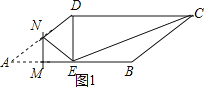
②当∠DEC＝90°，如图2，

过D作DH⊥AB于H，

∵AB∥CD，

∴∠HDC＝90°，

∴∠HDC+∠CDE＝∠CDE+∠DCE＝90°，

∴∠HDE＝∠DCE，

∴△DHE∽△CED，

∴，

∵sinA＝，AD＝10，

∴DH＝6，

∴AH＝8，

设HE＝x，

∴DE＝，

∵DH2+HE2＝DE2，

∴62+x2＝16x，

∴x＝8﹣2，x＝8+2(不合题意舍去)，

∴AE＝AH+HE＝16﹣2，

∴AM＝AE＝8﹣，

综上所述，AM的长为4或8﹣，

故答案为：4或8﹣．