
【题目】已知抛物线经过E(4,5),F(2,-3),G(-2,5),H(1,-4)四个点,选取其中两点用待定系数法能求出该抛物线解析式的是( )
A.E,FB.F,GC.F,HD.E,G
 教材全解字词句篇系列答案
教材全解字词句篇系列答案科目:初中数学 来源: 题型:
【题目】如图,平面直角坐标系中,△ABC为等边三角形,其中点A、B、C的坐标分别为(﹣3,﹣1)、(﹣3,﹣3)、(﹣3+![]() ,﹣2).现以y轴为对称轴作△ABC的对称图形,得△A1B1C1,再以x轴为对称轴作△A1B1C1的对称图形,得△A2B2C2.
,﹣2).现以y轴为对称轴作△ABC的对称图形,得△A1B1C1,再以x轴为对称轴作△A1B1C1的对称图形,得△A2B2C2.
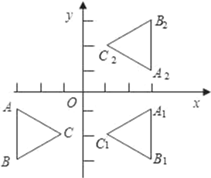
①直接写出点C1的坐标 ,点C2的坐标 ;
②能否通过一次旋转将△ABC旋转到△A2B2C2的位置?你若认为能,请作出肯定的回答,并直接写出所旋转的度数;你若认为不能,请作出否定的回答(不必说明理由);
③设当△ABC的位置发生变化时,△A2B2C2、△A1B1C1、△ABC之间的对称关系始终保持不变,当△ABC向上平移多少个单位时,△A1B1C1与△A2B2C2完全重合?并直接写出此时点C的坐标?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,E为BC上一点,DF⊥AE于F.

(1)ΔABE与ΔDFA相似吗?请说明理由;
(2)若AB=3,AD=6,BE=4,求DF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
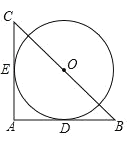
【题目】如图,在 Rt△ABC 中BC=2![]() ,以 BC 的中点 O 为圆心的⊙O 分别与 AB,AC 相切于 D,E 两点,
,以 BC 的中点 O 为圆心的⊙O 分别与 AB,AC 相切于 D,E 两点,![]() 的长为( )
的长为( )
A.![]() B.
B.![]() C.πD.2π
C.πD.2π
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y=2x+6与反比例数y=![]() (x>0)的图象交于点A(1,m),与x轴交于点B,与y轴交于点D.
(x>0)的图象交于点A(1,m),与x轴交于点B,与y轴交于点D.
(1)求m的值和反比例函数的表达式;
(2)观察图像,直接写出不等式2x+6-![]() >0的解集
>0的解集
(3)在反比例函数图像的第一象限上有一动点M,当S△BOM<S△BOD 时,直接写出点M纵坐标的的取值范围。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某单位为了创建城市文明单位,准备在单位的墙(线段MN所示)外开辟一处长方形的土地进行绿化美化,除墙体外三面要用栅栏围起来,计划用栅栏50米.
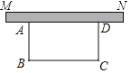
(1)不考虑墙体长度,问长方形的各边的长为多少时,长方形的面积最大?
(2)若墙体长度为20米,问长方形面积最大是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
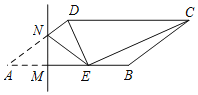
【题目】如图,已知ABCD中,AB=16,AD=10,sinA=![]() ,点M为AB边上一动点,过点M作MN⊥AB,交AD边于点N,将∠A沿直线MN翻折,点A落在线段AB上的点E处,当△CDE为直角三角形时,AM的长为_____.
,点M为AB边上一动点,过点M作MN⊥AB,交AD边于点N,将∠A沿直线MN翻折,点A落在线段AB上的点E处,当△CDE为直角三角形时,AM的长为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某超市销售水果时,将A、B、C三种水果采用甲、乙、丙三种方式搭配装箱进行销售,毎箱的成本分别为箱中A、B、C三种水果的成本之和,箱子成本忽略不计.甲种方式每箱分别装A、B、C三种水果6kg、3kg、1kg,乙种方式每分別裳A、B、C三种水果2kg、6kg、2kg,甲每箱的总成本是每千克A成本的15倍,每箱甲的销售利润率为20%,每箱甲比每箱乙的售价低25%;丙每箱在成本上提高40%标价后打八折销售获利为每千克A成本的1.2倍,当销售甲、乙、丙三种方式的水果数量之比为2:1:5时,则销售的总利润率为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若两个二次函数的图象的顶点、开口方向都相同,则称这两个二次函数为“同类二次函数”.
(1)请直接写出两个为“同类二次函数”的函数;
(2)已知关于x的二次函数y1=(x+2)2﹣3和y2=ax2+bx﹣1,若y1+y2与y1为“同类二次函数”,求函数y2的表达式,并求出当﹣3≤x≤0时,y2的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com