【题目】某超市销售水果时，将A、B、C三种水果采用甲、乙、丙三种方式搭配装箱进行销售，毎箱的成本分别为箱中A、B、C三种水果的成本之和，箱子成本忽略不计．甲种方式每箱分别装A、B、C三种水果6kg、3kg、1kg，乙种方式每分別裳A、B、C三种水果2kg、6kg、2kg，甲每箱的总成本是每千克A成本的15倍，每箱甲的销售利润率为20%，每箱甲比每箱乙的售价低25%；丙每箱在成本上提高40%标价后打八折销售获利为每千克A成本的1.2倍，当销售甲、乙、丙三种方式的水果数量之比为2：1：5时，则销售的总利润率为_____．
【答案】17.8%．
【解析】
分别设每千克A、B、C三种水果的成本为x、y、z，设丙每箱成本为m，然后根据题意将甲、乙、丙三种方式的每箱成本和利润用x表示出来即可求解．
解：设每千克A、B、C三种水果的成本分别为为x、y、z，依题意得：6x+3y+z＝12.5x，
∴3y+z＝6.5x，
∴每箱甲的销售利润＝12.5x20%＝2.5x
乙种方式每箱成本＝2x+6y+2z＝2x+13x＝15x，
乙种方式每箱售价＝12.5x（1+20%）÷（1﹣25%）＝20x，
∴每箱乙的销售利润＝20x﹣15x＝5x，
设丙每箱成本为m，依题意得：m（1+40%）0.8﹣m＝1.2x，
解得m＝10x．
∴当销售甲、乙、丙三种方式的水果数量之比为2：1：6时，
总成本为：12.5x2+15x1+10x5＝90x，
总利润为：2.5x2+5x+1.2x5＝16x，
销售的总利润率为
×100%≈17.8%，
故答案为：17.8%．
科目：初中数学 来源： 题型：
【题目】已知在平面直角坐标系xOy中（如图），抛物线y=ax2-4与x轴的负半轴相交于点A，与y轴相交于点B，AB=2
.点P在抛物线上，线段AP与y轴的正半轴交于点C，线段BP与x轴相交于点D，设点P的横坐标为m.
（1）求这条抛物线的解析式；
（2）用含m的代数式表示线段CO的长；
（3）当tan∠ODC=
时，求∠PAD的正弦值.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知抛物线经过E(4，5)，F（2，－3），G（－2，5），H（1，－4）四个点，选取其中两点用待定系数法能求出该抛物线解析式的是（ ）
A.E，FB.F，GC.F，HD.E，G
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】某商场购进一批单价为4元的日用品．若按每件5元的价格销售，每月能卖出3万件；若按每件6元的价格销售，每月能卖出2万件，假定每月销售件数y（件）与价格x（元/件）之间满足一次函数关系．
（1）试求y与x之间的函数关系式；
（2）当销售价格定为多少时，才能使每月的利润最大？每月的最大利润是多少？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在梯形
中，
，
，
.点
为边
的中点，以为顶点作
，射线
交腰
于点
，射线
交腰
于点
，联结
.
（1）求证：
；
（2）若
是以
为腰的等腰三角形，求的长；
（3）若
，求
的长.
查看答案和解析>>
科目：初中数学 来源： 题型：
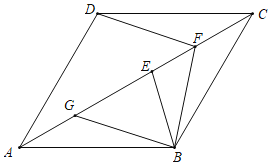
【题目】如图，四边形ABCD为菱形，∠BCD＝60°，E为对角线AC上一点，且AE＝AB，F为CE的中点，接DF、BF，BG⊥BF与AC交于点G；
（1）若AB＝2，求EF的长；
（2）求证：CG﹣EF＝
BG．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在ABCD中 过点A作AE⊥DC，垂足为E，连接BE，F为BE上一点，且∠AFE=∠D．
（1）求证：△ABF∽△BEC；
（2）若AD=5，AB=8，sinD=
，求AF的长．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，已知抛物线经过点A（﹣1，0），B（3，0），C（0，3）三点．
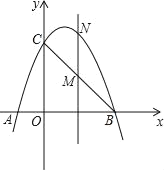
（1）求抛物线的解析式；
（2）点M是线段BC上的点（不与B、C重合），过M作NM∥y轴交抛物线于N，若点M的横坐标为m，请用含m的代数式表示MN的长；
（3）在（2）的条件下，连接NB，NC，是否存在点m，使△BNC的面积最大？若存在，求m的值和△BNC的面积；若不存在，说明理由
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】图中是抛物线形拱桥，点P处有一照明灯，水面OA宽4 m，以O为原点，OA所在直线为x轴建立平面直角坐标系，已知点P的坐标为（3，
）.
(1)点P与水面的距离是________m；
(2)求这条抛物线的表达式；
(3)当水面上升1 m后，水面的宽变为多少？
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com