
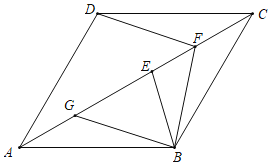
【题目】如图,四边形ABCD为菱形,∠BCD=60°,E为对角线AC上一点,且AE=AB,F为CE的中点,接DF、BF,BG⊥BF与AC交于点G;
(1)若AB=2,求EF的长;
(2)求证:CG﹣EF=![]() BG.
BG.
【答案】(1)![]() ﹣1;(2)详见解析.
﹣1;(2)详见解析.
【解析】
(1)连接BD交AC于O,由菱形的性质得出∠BAD=∠BCD=60°,AC⊥BD,OB=OD,OA=OC,∠OAB=![]() ∠BAD=30°,由直角三角形的性质得出OB=
∠BAD=30°,由直角三角形的性质得出OB=![]() AB=1,OA=
AB=1,OA=![]() OB=
OB=![]() ,得出AC=2OA=2
,得出AC=2OA=2![]() ,求出CE=AC﹣AE=2
,求出CE=AC﹣AE=2![]() ﹣2,即可得出答案;
﹣2,即可得出答案;
(2)设AB=2a,同(1)得OB=![]() AB=a,OA=
AB=a,OA=![]() OB=
OB=![]() a,得出AC=2OA=2
a,得出AC=2OA=2![]() a,求出CE=AC﹣AE=(2
a,求出CE=AC﹣AE=(2![]() ﹣2)a,OE=AE﹣OA=(2﹣
﹣2)a,OE=AE﹣OA=(2﹣![]() )a,得出OF=OE+EF=a,得出OB=OF,证出△BOF是等腰直角三角形,得出∠BFG=45°,证明△BFG是等腰直角三角形,得出GF=
)a,得出OF=OE+EF=a,得出OB=OF,证出△BOF是等腰直角三角形,得出∠BFG=45°,证明△BFG是等腰直角三角形,得出GF=![]() BG,即可得出结论.
BG,即可得出结论.
解:(1)连接BD交AC于O,如图所示:
∵四边形ABCD是菱形,
∴∠BAD=∠BCD=60°,AC⊥BD,OB=OD,OA=OC,∠OAB=![]() ∠BAD=30°,
∠BAD=30°,
∴OB=![]() AB=1,OA=
AB=1,OA=![]() OB=
OB=![]() ,
,
∴AC=2OA=2![]() ,
,
∵AE=AB=2,
∴CE=AC﹣AE=2![]() ﹣2,
﹣2,
∵F为CE的中点,
∴EF=![]() CE=
CE=![]() ﹣1;
﹣1;
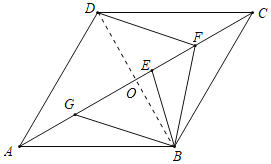
(2)证明:设AB=2a,
同(1)得:OB=![]() AB=a,OA=
AB=a,OA=![]() OB=
OB=![]() a,
a,
∴AC=2OA=2![]() a,
a,
∵AE=AB=2a,
∴CE=AC﹣AE=(2![]() ﹣2)a,OE=AE﹣OA=(2﹣
﹣2)a,OE=AE﹣OA=(2﹣![]() )a,
)a,
∵F为CE的中点,
∴EF=![]() CE=(
CE=(![]() ﹣1)a,
﹣1)a,
∴OF=OE+EF=(2﹣![]() )a+(
)a+(![]() ﹣1)a=a,
﹣1)a=a,
∴OB=OF,
∵AC⊥BD,
∴△BOF是等腰直角三角形,
∴∠BFG=45°,
∵BG⊥BF,
∴△BFG是等腰直角三角形,
∴GF=![]() BG,
BG,
∵GF=CG﹣CF=CG﹣EF,
∴CG﹣EF=![]() BG.
BG.


科目:初中数学 来源: 题型:
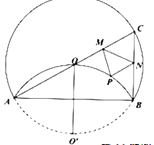
【题目】如图,将半径为4的![]() 沿弦
沿弦![]() 折叠,圆上点
折叠,圆上点![]() 折叠后恰好与圆点
折叠后恰好与圆点![]() 重合,连接
重合,连接![]() 并延长交
并延长交![]() 于点
于点![]() ,连接
,连接![]() .点
.点![]() 为弧
为弧![]() 上一点,
上一点,![]() 、
、![]() 分别为线段
分别为线段![]() 、
、![]() 上一动点,则
上一动点,则![]() 周长的最小值为___________.
周长的最小值为___________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某单位为了创建城市文明单位,准备在单位的墙(线段MN所示)外开辟一处长方形的土地进行绿化美化,除墙体外三面要用栅栏围起来,计划用栅栏50米.
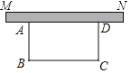
(1)不考虑墙体长度,问长方形的各边的长为多少时,长方形的面积最大?
(2)若墙体长度为20米,问长方形面积最大是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
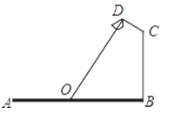
【题目】如图,要在宽为22米的大道两边安装路灯,路灯的灯臂CD长2米,且与灯柱BC成120°角,路灯采用圆锥形灯罩,灯罩的轴线DO与灯臂CD垂直,当灯罩的轴线DO通过公路路面的中心线时照明效果最佳,求路灯的灯柱BC高度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某超市销售水果时,将A、B、C三种水果采用甲、乙、丙三种方式搭配装箱进行销售,毎箱的成本分别为箱中A、B、C三种水果的成本之和,箱子成本忽略不计.甲种方式每箱分别装A、B、C三种水果6kg、3kg、1kg,乙种方式每分別裳A、B、C三种水果2kg、6kg、2kg,甲每箱的总成本是每千克A成本的15倍,每箱甲的销售利润率为20%,每箱甲比每箱乙的售价低25%;丙每箱在成本上提高40%标价后打八折销售获利为每千克A成本的1.2倍,当销售甲、乙、丙三种方式的水果数量之比为2:1:5时,则销售的总利润率为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,CD⊥AB,垂足为D,AF平分∠CAB,交CD于点E,交CB于点F.若AC=3,AB=5,则CE的长为( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
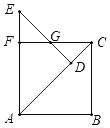
【题目】如图,在△ABC中,∠B=90°,AB=BC=4,把△ABC绕点A逆时针旋转45°得到△ADE,过点C作CF⊥AE于F,DE交CF于G,则四边形ADGF的周长是( )
A.8B.4+4![]() C.8+
C.8+![]() D.8
D.8![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
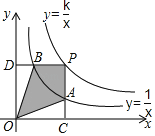
【题目】两个反比例函数y=![]() 和y=
和y=![]() 在第一象限内,点P在y=
在第一象限内,点P在y=![]() 的图象上,PC垂直于X轴于点C,交y=
的图象上,PC垂直于X轴于点C,交y=![]() 的图象于点A,PD垂直于Y轴于D,交y=
的图象于点A,PD垂直于Y轴于D,交y=![]() 的图象于点B,当点P在y=
的图象于点B,当点P在y=![]() 的图象上运动时,下列结论错误的是( )
的图象上运动时,下列结论错误的是( )
A.△ODB与△OCA的面积相等
B.当点A是PC的中点时,点B一定是PD的中点
C.只有当四边形OCPB为正方形时,四边形PAOB的面积最大
D.![]() =
=![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com