
【题目】两个反比例函数y=![]() 和y=
和y=![]() 在第一象限内,点P在y=
在第一象限内,点P在y=![]() 的图象上,PC垂直于X轴于点C,交y=
的图象上,PC垂直于X轴于点C,交y=![]() 的图象于点A,PD垂直于Y轴于D,交y=
的图象于点A,PD垂直于Y轴于D,交y=![]() 的图象于点B,当点P在y=
的图象于点B,当点P在y=![]() 的图象上运动时,下列结论错误的是( )
的图象上运动时,下列结论错误的是( )
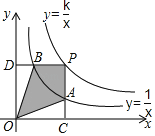
A.△ODB与△OCA的面积相等
B.当点A是PC的中点时,点B一定是PD的中点
C.只有当四边形OCPB为正方形时,四边形PAOB的面积最大
D.![]() =
=![]()
【答案】C
【解析】
根据反比例函数的图象和性质,特别是根据反比例函数k的几何意义,对四个选项逐一进行分析,即可得出正确答案.
A、由于点A和点D均在同一个反比例函数y=![]() 的图象上,所以S△ODB=
的图象上,所以S△ODB=![]() ,S△OCA=
,S△OCA=![]() ;故△ODB与△OCA的面积相等,故A正确;
;故△ODB与△OCA的面积相等,故A正确;
B、连接OP,点A是PC的中点,
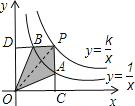
则△OAP和△OAC的面积相等,
∵△ODP的面积=△OCP的面积=![]() ,△ODB与△OCA的面积相等,
,△ODB与△OCA的面积相等,
∴△OBP与△OAP的面积相等,
∴△OBD和△OBP面积相等,
∴点B一定是PD的中点,故B正确;
C、由于矩形OCPD、三角形ODB、三角形OCA为定值,则四边形PAOB的面积不会发生变化,故C错误;
D、设P(m,![]() ),则A(m,
),则A(m,![]() ),B(
),B(![]() ,
,![]() ),则CA=
),则CA=![]() ,PA=
,PA=![]() ﹣
﹣![]() ,DB=
,DB=![]() ,PB=m﹣
,PB=m﹣![]() ,
,
故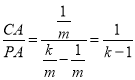 ,
,![]() ,
,
∴![]() ,故D正确.
,故D正确.
故选C.


科目:初中数学 来源: 题型:
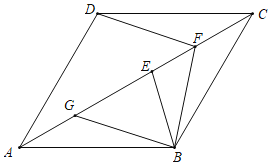
【题目】如图,四边形ABCD为菱形,∠BCD=60°,E为对角线AC上一点,且AE=AB,F为CE的中点,接DF、BF,BG⊥BF与AC交于点G;
(1)若AB=2,求EF的长;
(2)求证:CG﹣EF=![]() BG.
BG.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+2ax+3a2+3(其中x是自变量),当x≥2时,y随x的增大而增大,且-2≤x≤1时,y的最大值为9,则a的值为![]()
![]()
A. 1或![]() B. -
B. -![]() 或
或![]() C.
C. ![]() D. 1
D. 1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】包河区发展农业经济产业,在大圩乡种植多品种的葡萄.已知某葡萄种植户李大爷的葡萄成本为10元![]() ,如果在未来40天葡萄的销售单价
,如果在未来40天葡萄的销售单价![]() (元
(元![]() )与时间
)与时间![]() (天)之间的函数关系式为:
(天)之间的函数关系式为: ,且葡萄的日销售量
,且葡萄的日销售量![]() (千克)与时间
(千克)与时间![]() (天)的关系如下表:
(天)的关系如下表:
时间 | 1 | 3 | 6 | 10 | 20 | 40 |
日销售量 | 118 | 114 | 108 | 100 | 80 | 40 |
(1)请直接写出![]() 与
与![]() 之间的变化规律符合什么函数关系?并求在第15天的日销售量是多少千克?
之间的变化规律符合什么函数关系?并求在第15天的日销售量是多少千克?
(2)在后20天(即![]() ),请求出哪一天的日销售利润最大?日销售利润最大为多少?
),请求出哪一天的日销售利润最大?日销售利润最大为多少?
(3)在实际销售的前20天中,李大爷决定每销售1千克水果就捐赠![]() 元利润(
元利润(![]() )给留守贫困儿童作为助学金,前20天销售完后李大爷发现,每天扣除捐赠后的日销售利润随时间
)给留守贫困儿童作为助学金,前20天销售完后李大爷发现,每天扣除捐赠后的日销售利润随时间![]() 的增大而增大,请求出
的增大而增大,请求出![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】图中是抛物线形拱桥,点P处有一照明灯,水面OA宽4 m,以O为原点,OA所在直线为x轴建立平面直角坐标系,已知点P的坐标为(3,![]() ).
).
(1)点P与水面的距离是________m;
(2)求这条抛物线的表达式;
(3)当水面上升1 m后,水面的宽变为多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
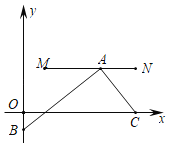
【题目】如图,在平面直角坐标系中,M、N、C三点的坐标分别为(![]() ,1),(3,1),(3,0),点A为线段MN上的一个动点,连接AC,过点A作AB⊥AC交y轴于点B,当点A从M运动到N时,点B随之运动,设点B的坐标为(0,b),则b的取值范围是( )
,1),(3,1),(3,0),点A为线段MN上的一个动点,连接AC,过点A作AB⊥AC交y轴于点B,当点A从M运动到N时,点B随之运动,设点B的坐标为(0,b),则b的取值范围是( )
A.![]() ≤b≤1B.
≤b≤1B.![]() ≤b≤1C.
≤b≤1C.![]() ≤b≤
≤b≤![]() D.
D.![]() ≤b≤1
≤b≤1
查看答案和解析>>
科目:初中数学 来源: 题型:
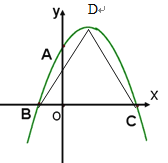
【题目】如图,二次函数![]() 图象与
图象与![]() 轴交于A、B与
轴交于A、B与![]() 轴交于C,OA=2,OB=1 ,OC=4
轴交于C,OA=2,OB=1 ,OC=4
(1).求二次函数解析式;
(2).若点D为抛物线的顶点,求△BCD的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某电视台为了解本地区电视节目的收视情况,对部分市民开展了“你最喜爱的电视节目”的问卷调查(每人只填写一项),根据收集的数据绘制了两幅不完整的统计图(如图所示),根据要求回答下列问题:
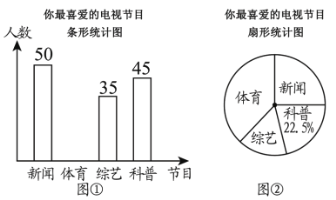
(1)本次问卷调查共调查了________名观众;图②中最喜爱“新闻节目”的人数占调查总人数的百分比为________;
(2)补全图①中的条形统计图;
(3)现有最喜爱“新闻节目”(记为![]() ),“体育节目”(记为
),“体育节目”(记为![]() ),“综艺节目”(记为
),“综艺节目”(记为![]() ),“科普节目”(记为
),“科普节目”(记为![]() )的观众各一名,电视台要从四人中随机抽取两人参加联谊活动,请用列表或画树状图的方法,求出恰好抽到最喜爱“
)的观众各一名,电视台要从四人中随机抽取两人参加联谊活动,请用列表或画树状图的方法,求出恰好抽到最喜爱“![]() ”和“
”和“![]() ”两位观众的概率.
”两位观众的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图![]() ,将菱形纸片
,将菱形纸片![]() 沿对角线
沿对角线![]() 剪开,得到
剪开,得到![]() 和
和![]() ,固定
,固定![]() ,并把
,并把![]() 与
与![]() 叠放在一起.
叠放在一起.

![]() 操作:如图
操作:如图![]() ,将
,将![]() 的顶点
的顶点![]() 固定在
固定在![]() 的
的![]() 边上的中点处,
边上的中点处,![]() 绕点
绕点![]() 在
在![]() 边上方左右旋转,设旋转时
边上方左右旋转,设旋转时![]() 交
交![]() 于点
于点![]() (
(![]() 点不与
点不与![]() 点重合),
点重合),![]() 交
交![]() 于点
于点![]() (
(![]() 点不与
点不与![]() 点重合).
点重合).
求证:![]()
![]() 操作:如图
操作:如图![]() ,
,![]() 的顶点
的顶点![]() 在
在![]() 的
的![]() 边上滑动(
边上滑动(![]() 点不与
点不与![]() 、
、![]() 点重合),且
点重合),且![]() 始终经过点
始终经过点![]() ,过点
,过点![]() 作
作![]() ,交
,交![]() 于点
于点![]() ,连接
,连接![]() .
.
探究:![]() ________.请予证明.
________.请予证明.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com