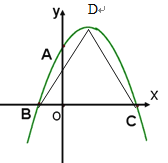
【题目】如图，二次函数
图象与
轴交于A、B与
轴交于C，OA=2，OB=1 ，OC=4
（1）.求二次函数解析式；
（2）.若点D为抛物线的顶点，求△BCD的面积.
【答案】（1）y=-
(x+1)(x-4)；（2）
【解析】
（1）先分别根据OA=2，OB=1 ，OC=4结合图象求得A,B,C的坐标，设交点式，将A点坐标代入即可求出函数解析式；
（2）根据B，C两点坐标可求得函数的对称轴，由此可求得函数的顶点坐标，根据三角形的面积公式计算面积即可.
解：(1)由题可知A(0,2),B(-1,0),C(4,0)
设函数解析式为y=a(x+1)(x-4)
代入A(0,2)得：2=a×1×（-4）
所以a=
所以函数解析式为：y=- (x+1)(x-4)
(2)(-1+4)÷2=
当x=时y=-×(+1) ×(-4)= 
所以顶点坐标为（，）
BC=OB+OC=1+4=5
所以S△BCD=×5×=
名校课堂系列答案科目：初中数学 来源： 题型：
【题目】如图，已知⊙O的半径为1，DE是⊙O的直径，过点D作⊙O的切线AD，C是AD的中点，AE交⊙O于B点，四边形BCOE是平行四边形．
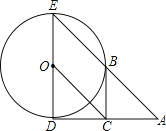
（1）求AD的长；
（2）BC是⊙O的切线吗？若是，给出证明；若不是，说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
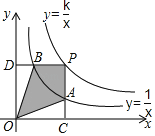
【题目】两个反比例函数y＝
和y＝
在第一象限内，点P在y＝的图象上，PC垂直于X轴于点C，交y＝的图象于点A，PD垂直于Y轴于D，交y＝的图象于点B，当点P在y＝的图象上运动时，下列结论错误的是（ ）
A.△ODB与△OCA的面积相等
B.当点A是PC的中点时，点B一定是PD的中点
C.只有当四边形OCPB为正方形时，四边形PAOB的面积最大
D.
＝
查看答案和解析>>
科目：初中数学 来源： 题型：
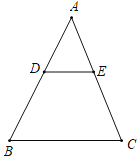
【题目】某施工地在道路拓宽施工时，遇到这样一个问题，马路旁边原有一个面积为100平方米，周长为90米的三角形绿化地，由于马路拓宽绿地被占去了一部分△ADE，变成了四边形BCED且DE∥BC，原绿化地一边AB的长由原来的30米缩短成BD为18米．求被占去的部分面积有多大？它的周长是多少？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】《九章算术》是中国传统数学最重要的著作，奠定了中国传统数学的基本框架．其中第九卷《勾股》章，主要讲述了以测量问题为中心的直角三角形三边互求的关系．其中记载：“今有邑，东西七里，南北九里，各中开门，出东门一十五里有木，问：出南门几何步而见木？”
译文：“今有一座长方形小城，东西向城墙长7里，南北向城墙长9里，各城墙正中均开一城门．走出东门15里处有棵大树，问走出南门多少步恰好能望见这棵树？”（注：1里＝300步）
你的计算结果是：出南门几何步而见木（ ）
A.300步B.315步C.400步D.415步
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】商店只有雪碧、可乐、果汁、奶汁四种饮料，每种饮料数量充足，某同学去该店购买饮料，每种饮料被选中的可能性相同．
（1）若他去买一瓶饮料，则他买到奶汁的概率是 ；
（2）若他两次去买饮料，每次买一瓶，且两次所买饮料品种不同，请用树状图或列表法求出他恰好买到雪碧和奶汁的概率．
查看答案和解析>>
科目：初中数学 来源： 题型：
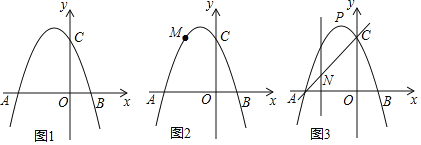
【题目】如图1所示，抛物线
交x轴于点
和点
，交y轴于点
．
求抛物线的函数表达式；
如图2所示，若点M是抛物线上一动点，且
，求点M的坐标；
如图3所示，设点N是线段AC上的一动点，作
轴，交抛物线于点P，求线段PN长度的最大值．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】一个不透明的布袋里装有4个大小、质地均相同的兵乓球，球上分别标有数字1、2、3、4
（1）随机从布袋中摸出一个兵乓球，记下数字后放回布袋里，再随机从布袋中摸出一个兵乓球，请用列表或画树状图的方式列出有可能的结果，并求出“两个兵乓球上的数字之和不小于4”的概率．
（2）随机从布袋中一次摸出两个兵乓球，直接写出“两个兵乓球上的数字至少有一个是奇数”的概率．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
