【题目】图中是抛物线形拱桥，点P处有一照明灯，水面OA宽4 m，以O为原点，OA所在直线为x轴建立平面直角坐标系，已知点P的坐标为（3，
）.
(1)点P与水面的距离是________m；
(2)求这条抛物线的表达式；
(3)当水面上升1 m后，水面的宽变为多少？
步步高达标卷系列答案科目：初中数学 来源： 题型：
【题目】如图，在平面直角坐标系中，Rt△ABC的顶点C在第一象限，顶点A、B的坐标分别为（1，0），（4，0），∠CAB=90°，BC=5．抛物线y=
+bx+c与边AC，y轴的交点的纵坐标分别为3，
．
（1）求抛物线y=+bx+c对应的函数关系式；
（2）若将抛物线y=+bx+c经过平移后的抛物线的顶点是边BC的中点，写出平移过程；
（3）若抛物线y=+bx+c平移后得到的抛物线y=
+k经过（﹣5，y1），（3，y2）两点，当y1＞y2＞k时，直接写出h的取值范围．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图
，
中，
，点
在
的延长线上，点
在
上，
，点
是
与
的交点，且
．
图中是否存在与
相等的角？若存在，请找出，并加以证明，若不存在，说明理由；
求证：
；
若将“点在的延长线上，点在上”和“点是与的交点，且”分别改为“点在
上，点在
的延长线上”和“点是
的延长线与的交点，且
”，其他条件不变（如图
）．当
，
时，求
的长（用含
、
的式子表示）．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】某公司根据市场计划调整投资策略，对
，
两种产品进行市场调查，收集数据如表：
项目 产品 | 年固定成本 （单位：万元） | 每件成本 （单位：万元） | 每件产品销售价 （万元） | 每年最多可生产的件数 |
|
|
|
|
|
|
|
|
|
|
其中
是待定常数，其值是由生产的材料的市场价格决定的，变化范围是
，销售产品时需缴纳
万元的关税，其中
为生产产品的件数，假定所有产品都能在当年售出，设生产，两种产品的年利润分别为
、
（万元），写出、与之间的函数关系式，注明其自变量的取值范围．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】二次函数y＝ax2＋bx＋c的图象如图所示，其对称轴为直线x＝1，有如下结论：
①c＜1；
②2a＋b＝0；
③b2＜4ac；
④若方程ax2＋bx＋c＝0的两根为x1，x2，则x1＋x2＝2.
其中正确的结论是( )
A. ①② B. ①③ C. ②④ D. ③④
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】（1）已知：如图1，点A、D、C、B在同一条直线上，AD＝BC，AE＝BF，CE＝DF，求证：AE∥BF．
（2）如图2所示，△ABC的顶点分别为A（﹣4，5），B（﹣3，2），C（4，﹣1）
①作出△ABC关于x轴对称的图形△A1B1C1；
②用三角板作出△ABC的AB边上的高CH．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】国家实行一系列“三农”优惠政策后，农民收入大幅度增加．某乡所辖村庄去年的年人均收入（单位：元）情况如下表：
年人均收入 | 3 500 | 3 700 | 3 800 | 3 900 | 4 500 |
村庄个数 | 1 | 1 | 3 | 3 | 1 |
该乡去年各村庄年人均收入的中位数是（ ）
A.3 700元B.3 800元C.3 850元D.3 900元
查看答案和解析>>
科目：初中数学 来源： 题型：
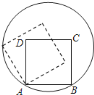
【题目】如图，边长为
的正方形
的顶点
、
在一个半径为的圆上，顶点
、
在圆内，将正方形沿圆的内壁逆时针方向作无滑动的滚动．当点第一次落在圆上时，点运动的路径长为________．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
