【题目】如图，在
中，
，
，
，点
为
的中点，以点为圆心作圆心角为
的扇形
，点
恰在弧
上，则图中阴影部分的面积为（ ）
A. 
B. 
C. 
D. 
【答案】D
【解析】
连接CD，作DM⊥BC，DN⊥AC，证明△DMG≌△DNH，则S四边形DGCH=S四边形DMCN，求得扇形FDE的面积，则阴影部分的面积即可求得．
连接CD，作DM⊥BC，DN⊥AC．
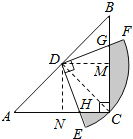
∵CA=CB，∠ACB=90°，点D为AB的中点，
∴DC=
AB=1，四边形DMCN是正方形，DM=
．
则扇形FDE的面积是：
．
∵CA=CB，∠ACB=90°，点D为AB的中点，
∴CD平分∠BCA，
又∵DM⊥BC，DN⊥AC，
∴DM=DN，
∵∠GDH=∠MDN=90°，
∴∠GDM=∠HDN，
则在△DMG和△DNH中，
，
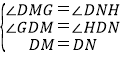∴△DMG≌△DNH（AAS），
∴S四边形DGCH=S四边形DMCN=．
则阴影部分的面积是：
-．
孟建平错题本系列答案
超能学典应用题题卡系列答案科目：初中数学 来源： 题型：
【题目】如图，在第一个△A1BC中，∠B＝30°，A1B＝CB，在边A1B上任取一D，延长CA2到A2，使A1A2＝A1D，得到第2个△A1A2D，在边A2B上任取一点E，延长A1A2到A3，使A2A3＝A2E，得到第三个△A2A3E，…按此做法继续下去，第n个等腰三角形的底角的度数是_____度．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图1，在线段BE上取一点C，分别以CB，CE为腰作等腰直角△BCA和等腰直角△DCE，连接BD和AE．
（1）请判断线段BD和线段AE的数量关系，并说明理由；
（2）如图2，若B，C，E三点不共线，（1）中的结论还成立吗？请说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】下面是小明同学设计的“作一个角等于已知角”的尺规作图过程.
已知：∠O，
求作：一个角，使它等于∠O.
作法：如图：
①在∠O的两边上分别任取一点A，B；
②以点A为圆心，OA为半径画弧；以点B为
圆心，OB为半径画弧；两弧交于点C；
③连结AC,BC ，所以∠C即为所求作的角.
请根据小明设计的尺规作图过程，
（1）使用直尺和圆规，补全图形；（保留作图痕迹）
（2）完成下列证明．
证明：连结AB，
∵OA=AC，OB= ， ，
∴
≌
（ ）（填推理依据）．
∴∠C=∠O．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】图中是抛物线形拱桥，点P处有一照明灯，水面OA宽4 m，以O为原点，OA所在直线为x轴建立平面直角坐标系，已知点P的坐标为（3，
）.
(1)点P与水面的距离是________m；
(2)求这条抛物线的表达式；
(3)当水面上升1 m后，水面的宽变为多少？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在平行四边形ABCD中，E、F分别在AD、BC边上，且AE=CF．
求证：（1）△ABE≌△CDF；
（2）四边形BFDE是平行四边形．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
