【题目】如图，在第一个△A1BC中，∠B＝30°，A1B＝CB，在边A1B上任取一D，延长CA2到A2，使A1A2＝A1D，得到第2个△A1A2D，在边A2B上任取一点E，延长A1A2到A3，使A2A3＝A2E，得到第三个△A2A3E，…按此做法继续下去，第n个等腰三角形的底角的度数是_____度．
全能测控期末小状元系列答案科目：初中数学 来源： 题型：
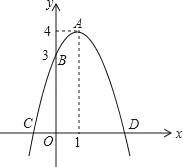
【题目】如图，已知抛物线的顶点为A(1，4)，抛物线与y轴交于点B(0，3)，与x轴交于C、D两点.点P是x轴上的一个动点.
(1)求此抛物线的解析式；
(2)当PA+PB的值最小时，求点P的坐标.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】问题背景：在△ABC中，AB、BC、AC三边的长分别为
、
、
，求这个三角形的面积小辉同学在解答这道题时，先建立一个正方形网格（每个小正方形的边长为1），再在网格中画出格点△ABC（即△ABC三个顶点都在小正方形的顶点处），如图1所示．这样不需求△ABC的高，而借用网格就能计算出它的面积．
（1）请你利用上述方法求出△ABC的面积．
（2）在图2中画△DEF，DE、EF、DF三边的长分别为
、
、
①判断三角形的形状，说明理由．
②求这个三角形的面积．（直接写出答案）
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】在△ABC中，AB=AC，在BC边上有两动点D、E，满足2∠DAE=∠BAC，将△AEC绕A旋转，使得AC与AB重合，点E落到点E’．
（1）求证：∠DAE’=∠DAE；
（2）当∠BE’D=20°时，求∠DEA的度数；
（3）当BD=1，EC=2，△BE’D又为直角三角形时，求∠BAC的度数．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在平面直角坐标系中，Rt△ABC的顶点C在第一象限，顶点A、B的坐标分别为（1，0），（4，0），∠CAB=90°，BC=5．抛物线y=
+bx+c与边AC，y轴的交点的纵坐标分别为3，
．
（1）求抛物线y=+bx+c对应的函数关系式；
（2）若将抛物线y=+bx+c经过平移后的抛物线的顶点是边BC的中点，写出平移过程；
（3）若抛物线y=+bx+c平移后得到的抛物线y=
+k经过（﹣5，y1），（3，y2）两点，当y1＞y2＞k时，直接写出h的取值范围．
查看答案和解析>>
科目：初中数学 来源： 题型：
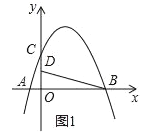
【题目】如图，在平面直角坐标系中，抛物线y=ax2+bx+4交x轴于点A（﹣2，0）和B（B在A右侧），交y轴于点C，直线y=
经过点B，交y轴于点D，且D为OC中点．
（1）求抛物线的解析式；
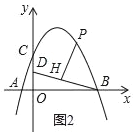
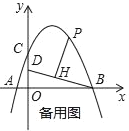
（2）若P是第一象限抛物线上的一点，过P点作PH⊥BD于H，设P点的横坐标是t，线段PH的长度是d，求d与t的函数关系式；
（3）在（2）的条件下，当d=
时，将射线PH绕着点P顺时针方向旋转45°交抛物线于点Q，求点Q的坐标．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
