
【题目】如图,在平面直角坐标系中,Rt△ABC的顶点C在第一象限,顶点A、B的坐标分别为(1,0),(4,0),∠CAB=90°,BC=5.抛物线y=![]() +bx+c与边AC,y轴的交点的纵坐标分别为3,
+bx+c与边AC,y轴的交点的纵坐标分别为3,![]() .
.
(1)求抛物线y=![]() +bx+c对应的函数关系式;
+bx+c对应的函数关系式;
(2)若将抛物线y=![]() +bx+c经过平移后的抛物线的顶点是边BC的中点,写出平移过程;
+bx+c经过平移后的抛物线的顶点是边BC的中点,写出平移过程;
(3)若抛物线y=![]() +bx+c平移后得到的抛物线y=
+bx+c平移后得到的抛物线y=![]() +k经过(﹣5,y1),(3,y2)两点,当y1>y2>k时,直接写出h的取值范围.
+k经过(﹣5,y1),(3,y2)两点,当y1>y2>k时,直接写出h的取值范围.

【答案】(1)y=![]() +x+
+x+![]() ;(2)将y=
;(2)将y=![]() (x+1)2+1向右平移3.5个单位长度,再向上平移1个单位长度后得到抛物线的顶点是边BC的中点;(3)h的取值范围为h>﹣1且h≠3
(x+1)2+1向右平移3.5个单位长度,再向上平移1个单位长度后得到抛物线的顶点是边BC的中点;(3)h的取值范围为h>﹣1且h≠3
【解析】
(1)根据抛物线y=![]() x2+bx+c与边AC,y轴的交点的纵坐标分别为3,
x2+bx+c与边AC,y轴的交点的纵坐标分别为3,![]() ,可得抛物线y=
,可得抛物线y=![]() x2+bx+c过点(1,3),(0,
x2+bx+c过点(1,3),(0,![]() ),根据待定系数法可求抛物线y=
),根据待定系数法可求抛物线y=![]() x2+bx+c对应的函数关系式;
x2+bx+c对应的函数关系式;
(2)根据勾股定理可求AC的长,可得C点坐标,进一步得到BC中点的坐标为(2.5,2),将y=![]() x2+x+
x2+x+![]() 配方得y=
配方得y=![]() (x+1)2+1,依此即可写出平移过程;
(x+1)2+1,依此即可写出平移过程;
(3)先求出抛物线y=![]() x2+x+
x2+x+![]() =
=![]() (x+1)2+1的对称轴为x=-1,可得h的取值范围.
(x+1)2+1的对称轴为x=-1,可得h的取值范围.
(1)∵抛物线y=![]() +bx+c与边AC,y轴的交点的纵坐标分别为3,
+bx+c与边AC,y轴的交点的纵坐标分别为3,![]() .
.
∴抛物线y=![]() +bx+c过点(1,3),(0,
+bx+c过点(1,3),(0,![]() ),
),
把点(1,3),(0,![]() )代入y=
)代入y=![]() +bx+c得
+bx+c得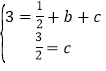 .
.
∴ ,
,
∴抛物线y=![]() +bx+c对应的函数关系式为:y=
+bx+c对应的函数关系式为:y=![]() +x+
+x+![]() ;
;
(2)在Rt△ABC中,∵∠CAB=90°,AB=4﹣1=3,BC=5,
∴AC=![]() ,
,
∴C(1,4),
∴BC中点的坐标为(2.5,2),
将y=![]() +x+
+x+![]() 配方得,y=
配方得,y=![]() (x+1)2+1,
(x+1)2+1,
∴将y=![]() (x+1)2+1向右平移3.5个单位长度,再向上平移1个单位长度后得到抛物线的顶点是边BC的中点;
(x+1)2+1向右平移3.5个单位长度,再向上平移1个单位长度后得到抛物线的顶点是边BC的中点;
(3)∵抛物线y=![]() +x+
+x+![]() =
=![]() (x+1)2+1的对称轴为x=﹣1,抛物线y=
(x+1)2+1的对称轴为x=﹣1,抛物线y=![]() +bx+c平移后得到的抛物线y=
+bx+c平移后得到的抛物线y=![]() +k经过(﹣5,y1),(3,y2)两点,
+k经过(﹣5,y1),(3,y2)两点,
∴h的取值范围为h>﹣1且h≠3.


科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx+c的图象如图所示,对称轴为直线x=1,则下列结论正确的是( )

A. ac>0 B. 当x>0时,y随x的增大而减小
C. 2a﹣b=0 D. 方程ax2+bx+c=0的两根是x1=﹣1,x2=3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,∠1=∠2,则不一定能使△ABD≌△ACD的条件是 ( )

A. AB=AC B. BD=CD C. ∠B=∠C D. ∠BDA=∠CDA
查看答案和解析>>
科目:初中数学 来源: 题型:
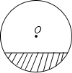
【题目】一根水平放置的圆柱形输水管道的横截面如图所示,其中有水部分水面宽![]() 米,最深处水深
米,最深处水深![]() 米,则此输水管道的直径等于( )
米,则此输水管道的直径等于( )
A. ![]() 米 B.
米 B. ![]() 米 C.
米 C. ![]() 米 D.
米 D. ![]() 米
米
查看答案和解析>>
科目:初中数学 来源: 题型:
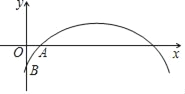
【题目】如图,已知二次函数y1=ax2+bx+c的图象分别与x轴的正半轴、y轴的负半轴于A、B两点,且OA=OB,则一次函数y2=(ac﹣b)x+abc的图象可能是( )
A. 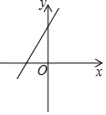 B.
B. 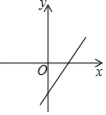 C.
C. 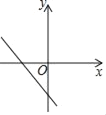 D.
D. 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在第一个△A1BC中,∠B=30°,A1B=CB,在边A1B上任取一D,延长CA2到A2,使A1A2=A1D,得到第2个△A1A2D,在边A2B上任取一点E,延长A1A2到A3,使A2A3=A2E,得到第三个△A2A3E,…按此做法继续下去,第n个等腰三角形的底角的度数是_____度.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,△ABC的一边AB在x轴上,∠ABC=90°,点C(4,8)在第一象限内,AC与y轴交于点E,抛物线y=![]() +bx+c经过A、B两点,与y轴交于点D(0,﹣6).
+bx+c经过A、B两点,与y轴交于点D(0,﹣6).

(1)请直接写出抛物线的表达式;
(2)求ED的长;
(3)点P是x轴下方抛物线上一动点,设点P的横坐标为m,△PAC的面积为S,试求出S与m的函数关系式;
(4)若点M是x轴上一点(不与点A重合),抛物线上是否存在点N,使∠CAN=∠MAN.若存在,请直接写出点N的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1) 观察被开方数a的小数点与算术平方根![]() 的小数点的移动规律:
的小数点的移动规律:
a | 0.0001 | 0.01 | 1 | 100 | 10000 |
| 0.01 | x | 1 | y | 100 |
填空:x= _______, y=______.
(2)根据你发现的规律填空:
①已知![]() ≈1.414,则
≈1.414,则![]() =________,
=________,![]() =_______;
=_______;
②![]() = 0.274,记
= 0.274,记![]() 的整数部分为x,则
的整数部分为x,则![]() =___________.
=___________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】图中是抛物线形拱桥,点P处有一照明灯,水面OA宽4 m,以O为原点,OA所在直线为x轴建立平面直角坐标系,已知点P的坐标为(3,![]() ).
).
(1)点P与水面的距离是________m;
(2)求这条抛物线的表达式;
(3)当水面上升1 m后,水面的宽变为多少?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com