
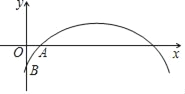
【题目】如图,已知二次函数y1=ax2+bx+c的图象分别与x轴的正半轴、y轴的负半轴于A、B两点,且OA=OB,则一次函数y2=(ac﹣b)x+abc的图象可能是( )
A. 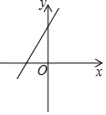 B.
B. 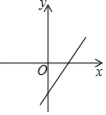 C.
C. 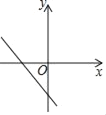 D.
D. 
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】某所中学七、八、九年级各有6个班级,每个班级人数为50左右,根据实际情况,决定开设“A:乒乓球,B:篮球,C:跑步,D:跳绳”这四种项目.为了解学生喜欢哪一种项目,该学校体育组随机抽取了部分学生进行调查,并将调查结果绘制成如图所示的条形统计图和扇形统计图.请结合图中信息解答下列问题:
(1)样本容量是________,请你为体育组提供一种较为合理的抽样方案;
(2)把条形统计图补充完整;
(3)该校贝贝、晶晶、洋洋和妮妮是学校的校园之星,现要从这四人中选出两人作为“阳光体育”运动形象代言人,贝贝和晶晶同时被抽到的概率是多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在边长为1个单位长度的小正方形组成的网格中,点A、B、C在小正方形的顶点上.

(1)![]() 的面积为_______________;(请写出作答步骤)
的面积为_______________;(请写出作答步骤)
(2)在图中画出![]() 与
与![]() 关于直线l成轴对称的;
关于直线l成轴对称的;
(3)在直线l上找一点P,使PA+PB的长最短,则这个最短长度的平方为__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知如图,在射线AB上依次作正方形A1B1B2C1、正方形A2B2B3C2、正方形A3B3B4C3…,点A1,A2,A3,…在射线OA上,点B1,B2,B3,…在射线OB上,若AB1=A1B1=1,则正方形AnBnBn+1Cn的边长为 _______.

查看答案和解析>>
科目:初中数学 来源: 题型:
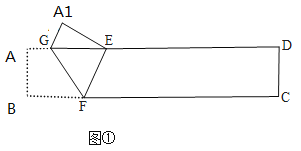
【题目】四边形ABCD是长方形,将长方形ABCD折叠,如图①所示,点B落在AD边上的点E处,折痕为FG,将图②折叠,点C与点E重合,折痕为PH.
(1)在图②中,证明:EH=EP;
(2)若EF=6,EH=8,FH=10,求长方形ABCD的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,Rt△ABC的顶点C在第一象限,顶点A、B的坐标分别为(1,0),(4,0),∠CAB=90°,BC=5.抛物线y=![]() +bx+c与边AC,y轴的交点的纵坐标分别为3,
+bx+c与边AC,y轴的交点的纵坐标分别为3,![]() .
.
(1)求抛物线y=![]() +bx+c对应的函数关系式;
+bx+c对应的函数关系式;
(2)若将抛物线y=![]() +bx+c经过平移后的抛物线的顶点是边BC的中点,写出平移过程;
+bx+c经过平移后的抛物线的顶点是边BC的中点,写出平移过程;
(3)若抛物线y=![]() +bx+c平移后得到的抛物线y=
+bx+c平移后得到的抛物线y=![]() +k经过(﹣5,y1),(3,y2)两点,当y1>y2>k时,直接写出h的取值范围.
+k经过(﹣5,y1),(3,y2)两点,当y1>y2>k时,直接写出h的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,△ABD,△ACE都是等边三角形,
(1)求证:△ABE≌△ADC;
(2)若∠ACD=15°,求∠AEB的度数;
(3)如图2,当△ABD与△ACE的位置发生变化,使C、E、D三点在一条直线上,求证:AC∥BE.

查看答案和解析>>
科目:初中数学 来源: 题型:
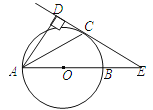
【题目】如图,已知AB是⊙O的直径,锐角∠DAB的平分线AC交⊙O于点C,作CD⊥AD,垂足为D,直线CD与AB的延长线交于点E.
(1)求证:直线CD为⊙O的切线;
(2)当AB=2BE,且CE=时,求AD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c的图象如图所示,其对称轴为直线x=1,有如下结论:
①c<1;
②2a+b=0;
③b2<4ac;
④若方程ax2+bx+c=0的两根为x1,x2,则x1+x2=2.

其中正确的结论是( )
A. ①② B. ①③ C. ②④ D. ③④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com