
【题目】已知如图,在射线AB上依次作正方形A1B1B2C1、正方形A2B2B3C2、正方形A3B3B4C3…,点A1,A2,A3,…在射线OA上,点B1,B2,B3,…在射线OB上,若AB1=A1B1=1,则正方形AnBnBn+1Cn的边长为 _______.

科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,直线l1的解析式为y=x,直线l2的解析式为y=-![]() x+3,与x轴、y轴分别交于点A、点B,直线l1与l2交于点C.点P是y轴上一点.
x+3,与x轴、y轴分别交于点A、点B,直线l1与l2交于点C.点P是y轴上一点.

(1)写出下列各点的坐标:点A( , )、点B( , )、点C( , );
(2)若S△COP=S△COA,请求出点P的坐标;
(3)当PA+PC最短时,求出直线PC的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小军和小明玩一种抽卡片游戏,他们拿了八张扑克牌,将数字为![]() 、
、![]() 、
、![]() 、
、![]() 的四张牌给小军,将数字为
的四张牌给小军,将数字为![]() 、
、![]() 、
、![]() 、
、![]() 的四张牌给小明,并按如下游戏规则进行:小军和小明各自的四张牌中随机抽出一张,然后将抽出的两张牌数字相加,若和为偶数,小军赢,若和为奇数,则小明赢.
的四张牌给小明,并按如下游戏规则进行:小军和小明各自的四张牌中随机抽出一张,然后将抽出的两张牌数字相加,若和为偶数,小军赢,若和为奇数,则小明赢.
![]() 请用树状图或列表法求小军获胜的概率.
请用树状图或列表法求小军获胜的概率.
![]() 这个游戏公平吗?请说明理由.
这个游戏公平吗?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,∠1=∠2,则不一定能使△ABD≌△ACD的条件是 ( )

A. AB=AC B. BD=CD C. ∠B=∠C D. ∠BDA=∠CDA
查看答案和解析>>
科目:初中数学 来源: 题型:
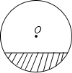
【题目】一根水平放置的圆柱形输水管道的横截面如图所示,其中有水部分水面宽![]() 米,最深处水深
米,最深处水深![]() 米,则此输水管道的直径等于( )
米,则此输水管道的直径等于( )
A. ![]() 米 B.
米 B. ![]() 米 C.
米 C. ![]() 米 D.
米 D. ![]() 米
米
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知二次函数y1=ax2+bx+c的图象分别与x轴的正半轴、y轴的负半轴于A、B两点,且OA=OB,则一次函数y2=(ac﹣b)x+abc的图象可能是( )
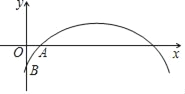
A. 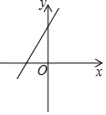 B.
B. 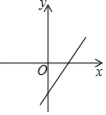 C.
C. 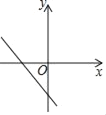 D.
D. 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,△ABC的一边AB在x轴上,∠ABC=90°,点C(4,8)在第一象限内,AC与y轴交于点E,抛物线y=![]() +bx+c经过A、B两点,与y轴交于点D(0,﹣6).
+bx+c经过A、B两点,与y轴交于点D(0,﹣6).

(1)请直接写出抛物线的表达式;
(2)求ED的长;
(3)点P是x轴下方抛物线上一动点,设点P的横坐标为m,△PAC的面积为S,试求出S与m的函数关系式;
(4)若点M是x轴上一点(不与点A重合),抛物线上是否存在点N,使∠CAN=∠MAN.若存在,请直接写出点N的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】莆田元宵节从农历正月初六持续到正月廿九,堪称全国最长的元宵节,其中江东桔塔和延宁蔗塔十分引人关注.元宵节前夕,江东村和延宁村置办元宵节所需的桔子和甘蔗中,桔子重量比甘蔗重量少100千克.若市场上每千克桔子的价格是甘蔗的1.5倍,所采购桔子和甘蔗的费用都是1200元,求每千克桔子和甘蔗分别是多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com