Question

【题目】如图，在平面直角坐标系中，直线l1的解析式为y＝x，直线l2的解析式为y＝－x＋3，与x轴、y轴分别交于点A、点B，直线l1与l2交于点C.点P是y轴上一点.

(1)写出下列各点的坐标：点A( ， )、点B( ， )、点C( ， )；

(2)若S△COP＝S△COA,请求出点P的坐标；

(3)当PA＋PC最短时，求出直线PC的解析式.

Answer 1

【答案】（1）A（6，0），B（0,3），C（2,2）；(2) P（0，）；（3）直线PC的解析式为

【解析】

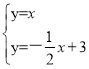（1）x=0代入，即可求出点A坐标，把y=0代入即可求出点B坐标，求方程组的解即可求出点C的坐标；

(2)设P点坐标为（0，y），根据S△COP＝S△COA列方程求解即可，

（3）作点C关于y轴的对称点为M（﹣2，2），求出过点A，M的直线解析式，再求直线AM与y轴的交点坐标，即求出P的坐标，即可求出直线PC的解析式.

（1）把x=0代入，

∴y=3，∴B（0,3），

把y=0代入，∴x=6，A（6，0），

且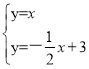，∴C点坐标为（2,2），

（2）∵A（6，0），C（2,2）∴S△COA,=6×2÷2=6；

∵P是y轴上一点，∴设P的坐标为（0，y），

∴S△COP=，∵S△COP＝S△COA，

∴=6，∴y=±6，

∴P（0,6）或（0，﹣6）.

（3）如图，过点C作y轴的对称点M，连接AM与y轴交与点P，则此时PA＋PC最短，

∵C的坐标为C（2,2），∴点C关于y轴的对称点为M（﹣2，2），

∴过点A，M的直线解析式为 ，

∵直线AM与y轴的交点为P（0，），

∴当P点坐标为（0，）时，PA＋PC最短，

∴直线PC的解析式为.