
ЁОЬтФПЁПШчЭМЃЌдкЦНУцжБНЧзјБъЯЕxOyжаЃЌвджБЯпx=![]() ЖдГЦжсЕФХзЮяЯпy=ax2+bx+cгыжБЯпlЃКy=kx+mЃЈkЃО0ЃЉНЛгкAЃЈ1ЃЌ1ЃЉЃЌBСНЕуЃЌгыyжсНЛгкCЃЈ0ЃЌ5ЃЉЃЌжБЯпlгыyжсНЛгкЕуDЃЎ
ЖдГЦжсЕФХзЮяЯпy=ax2+bx+cгыжБЯпlЃКy=kx+mЃЈkЃО0ЃЉНЛгкAЃЈ1ЃЌ1ЃЉЃЌBСНЕуЃЌгыyжсНЛгкCЃЈ0ЃЌ5ЃЉЃЌжБЯпlгыyжсНЛгкЕуDЃЎ
ЃЈ1ЃЉЧѓХзЮяЯпЕФКЏЪ§БэДяЪНЃЛ
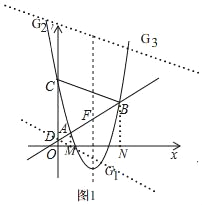
ЃЈ2ЃЉЩшжБЯпlгыХзЮяЯпЕФЖдГЦжсЕФНЛЕуЮЊFЃЌGЪЧХзЮяЯпЩЯЮЛгкЖдГЦжсгвВрЕФвЛЕуЃЌШє![]() ЃЌЧвЁїBCGгыЁїBCDУцЛ§ЯрЕШЃЌЧѓЕуGЕФзјБъЃЛ
ЃЌЧвЁїBCGгыЁїBCDУцЛ§ЯрЕШЃЌЧѓЕуGЕФзјБъЃЛ
ЃЈ3ЃЉШєдкxжсЩЯгаЧвНігавЛЕуPЃЌЪЙЁЯAPB=90ЁуЃЌЧѓkЕФжЕЃЎ

ЁОД№АИЁПЃЈ1ЃЉy=x2Љ5x+5ЃЌЃЈ2ЃЉGЃЈ3ЃЌЉ1ЃЉЃЌGЃЈ![]() ЃЌ
ЃЌ![]() ЃЉЃЎЃЈ3ЃЉЉ1+
ЃЉЃЎЃЈ3ЃЉЉ1+![]()
ЃЎ
ЁОНтЮіЁП
ЃЈ1ЃЉИљОнЖўДЮКЏЪ§ЕФЭМЯѓгыЯЕЪ§ЕФЙиЯЕСаГіЗНГЬзщНтГіaЃЌbЃЌcЕФжЕМДЕУЖўДЮКЏЪ§ЕФНтЮіЪНЃЛ
ЃЈ2ЃЉзїAMЁЭxжсЃЌBNЁЭxжсЃЌДЙзуЗжБ№ЮЊMЃЌNЃЌПЩЕУГіBЕуЕФзјБъМДПЩСаГіЗНГЬзщЧѓГівЛДЮКЏЪ§НтЮіЪНЃЌдйИљОнSЁїBCD=SЁїBCGСаГіЕШЪНМДПЩЧѓЕУGЃЛ
ЃЈ3ЃЉИљОнЬтвтСаГіЕШЪНЧѓГіxЕФжЕЃЌдђBЃЈk+4ЃЌk2+3k+1ЃЉЃЌдйИљОнвдABЮЊжБОЖЕФдВгыxжсжЛгавЛИіНЛЕуЃЌЧвPЮЊЧаЕуЃЌЕУГіOЁфPЁЭxжсЃЌPЃЈ![]() ЃЌ0ЃЉЃЌИљОнЁїAMPЁзЁїPNBЃЌЕУГіAMBN=PNPMЃЌДњШыЪ§жЕМДПЩЧѓГіkЕФжЕ.
ЃЌ0ЃЉЃЌИљОнЁїAMPЁзЁїPNBЃЌЕУГіAMBN=PNPMЃЌДњШыЪ§жЕМДПЩЧѓГіkЕФжЕ.
НтЃКЃЈ1ЃЉгЩЬтвтПЩЕУ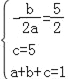 ЃЌ
ЃЌ
НтЕУa=1ЃЌb=Љ5ЃЌc=5ЃЛ
ЁрЖўДЮКЏЪ§ЕФНтЮіЪНЮЊЃКy=x2Љ5x+5ЃЌ
ЃЈ2ЃЉзїAMЁЭxжсЃЌBNЁЭxжсЃЌДЙзуЗжБ№ЮЊMЃЌNЃЌ
дђ![]() ЃЌ
ЃЌ
ЁпMQ=![]() ЃЌ
ЃЌ
ЁрNQ=2ЃЌBЃЈ![]() ЃЌ
ЃЌ![]() ЃЉЃЛ
ЃЉЃЛ
Ёр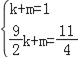 ЃЌ
ЃЌ
НтЕУ![]() ЃЌ
ЃЌ
Ёр![]() ЃЌDЃЈ0ЃЌ
ЃЌDЃЈ0ЃЌ![]() ЃЉЃЌ
ЃЉЃЌ
ЭЌРэПЩЧѓЃЌ![]() ЃЌ
ЃЌ
ЁпSЁїBCD=SЁїBCGЃЌ
ЁрЂйDGЁЮBCЃЈGдкBCЯТЗНЃЉЃЌ![]() ЃЌ
ЃЌ
Ёр![]() =x2Љ5x+5ЃЌ
=x2Љ5x+5ЃЌ
НтЕУЃЌ![]() ЃЌx2=3ЃЌ
ЃЌx2=3ЃЌ
ЁпxЃО![]() ЃЌ
ЃЌ
Ёрx=3ЃЌ
ЁрGЃЈ3ЃЌЉ1ЃЉЃЎ
ЂкGдкBCЩЯЗНЪБЃЌжБЯпG2G3гыDG1ЙигкBCЖдГЦЃЌ
Ёр![]() =
=![]() ЃЌ
ЃЌ
Ёр![]() =x2Љ5x+5ЃЌ
=x2Љ5x+5ЃЌ
НтЕУ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ
ЁпxЃО![]() ЃЌ
ЃЌ
Ёрx=![]() ЃЌ
ЃЌ
ЁрGЃЈ![]() ЃЌ
ЃЌ![]() ЃЉЃЌ
ЃЉЃЌ
злЩЯЫљЪіЕуGЕФзјБъЮЊGЃЈ3ЃЌЉ1ЃЉЃЌGЃЈ![]() ЃЌ
ЃЌ![]() ЃЉЃЎ
ЃЉЃЎ
ЃЈ3ЃЉгЩЬтвтПЩжЊЃКk+m=1ЃЌ
Ёрm=1ЉkЃЌ
Ёрyl=kx+1ЉkЃЌ
Ёрkx+1Љk=x2Љ5x+5ЃЌ
НтЕУЃЌx1=1ЃЌx2=k+4ЃЌ
ЁрBЃЈk+4ЃЌk2+3k+1ЃЉЃЌ
ЩшABжаЕуЮЊOЁфЃЌ
ЁпPЕугаЧвжЛгавЛИіЃЌ
ЁрвдABЮЊжБОЖЕФдВгыxжсжЛгавЛИіНЛЕуЃЌЧвPЮЊЧаЕуЃЌ
ЁрOЁфPЁЭxжсЃЌ
ЁрPЮЊMNЕФжаЕуЃЌ
ЁрPЃЈ![]() ЃЌ0ЃЉЃЌ
ЃЌ0ЃЉЃЌ
ЁпЁїAMPЁзЁїPNBЃЌ
Ёр![]() ЃЌ
ЃЌ
ЁрAMBN=PNPMЃЌ
Ёр1ЁСЃЈk2+3k+1ЃЉ=ЃЈk+4Љ![]() ЃЉЃЈ
ЃЉЃЈ![]() ЃЉЃЌ
ЃЉЃЌ
ЁпkЃО0ЃЌ
Ёрk=![]() =Љ1+
=Љ1+![]() ЃЎ
ЃЎ


 дФЖСПьГЕЯЕСаД№АИ
дФЖСПьГЕЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдкШеРњЩЯЮвУЧПЩвдЗЂЯжЦфжаФГаЉЪ§ТњзувЛЖЈЕФЙцТЩ.ШчЭМЪЧ2018Фъ8дТЗнЕФШеРњЃЌЮвУЧШЮвтбЁдёЦфжаЫљЪОЕФЗНПђВПЗжЃЌНЋЗНПђВПЗжжаЕФ4ИіЮЛжУЕФЪ§НЛВцЯрГЫЃЌдйЯрМѕЃЌШч8ЁС16Ѓ9ЁС15=Ѓ7,19ЁС27Ѓ20ЁС26=Ѓ7ЃЌВЛФбЗЂЯжНсЙћЖМЪЧЃ7.
ЃЈ1ЃЉЧыФудйбЁдёвЛзщЪ§АДЩЯУцЕФЗНЪНМЦЫуЃЌПДПДЪЧЗёЗћКЯетИіЙцТЩ.ВЂгУФуЩУГЄЕФБэДяЗНЪНУшЪіетИіЙцТЩ.
ЃЈ2ЃЉЧыФуРћгУећЪНЕФдЫЫуЖдвдЩЯЕФЙцТЩМгвджЄУї.

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЂйЕФГЄЗНаЮABCDжаЃЌ EдкADЩЯЃЌбиBEНЋAЕуЭљгвелГЩШчЭМЂкЫљЪОЃЌдйзїAFЁЭCDгкЕуFЃЌШчЭМЂлЫљЪОЃЌШєABЃН2ЃЌBCЃН3ЃЌЁЯBEAЃН60ЁуЃЌдђЭМЂлжаAFЕФГЄЖШЮЊ_______ЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЯТУцЪЧПЮБОжаЁАзївЛИіНЧЕШгквбжЊНЧЁБЕФГпЙцзїЭМЙ§ГЬЃЎвбжЊЃКЁЯAOBЃЎ ЧѓзїЃКвЛИіНЧЃЌЪЙЫќЕШгкЁЯAOBЃЎзїЗЈЃКШчЭМ
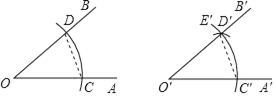
ЃЈ1ЃЉзїЩфЯпO'A'ЃЛ
ЃЈ2ЃЉвдOЮЊдВаФЃЌШЮвтГЄЮЊАыОЖзїЛЁЃЌНЛOAгкCЃЌНЛOBгкDЃЛ
ЃЈ3ЃЉвдO'ЮЊдВаФЃЌOCЮЊАыОЖзїЛЁC'E'ЃЌНЛO'A'гкC'ЃЛ
ЃЈ4ЃЉвдC'ЮЊдВаФЃЌCDЮЊАыОЖзїЛЁЃЌНЛЛЁC'E'гкD'ЃЛ
ЃЈ5ЃЉЙ§ЕуD'зїЩфЯпO'B'ЃЎ
дђЁЯA'O'B'ОЭЪЧЫљЧѓзїЕФНЧЃЎ
ЧыЛиД№ЃКИУзїЭМЕФвРОнЪЧЃЈЁЁЁЁЃЉ
A.SSSB.SASC.ASAD.AAS
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌвбжЊе§БШР§КЏЪ§y=2xгыЗДБШР§КЏЪ§y=![]() ЃЈkЃО0ЃЉЕФЭМЯѓНЛгкAЁЂBСНЕуЃЌЧвЕуAЕФКсзјБъЮЊ4ЃЌ
ЃЈkЃО0ЃЉЕФЭМЯѓНЛгкAЁЂBСНЕуЃЌЧвЕуAЕФКсзјБъЮЊ4ЃЌ
ЃЈ1ЃЉЧѓkЕФжЕЃЛ
ЃЈ2ЃЉИљОнЭМЯѓжБНгаДГіе§БШР§КЏЪ§жЕаЁгкЗДБШР§КЏЪ§жЕЪБxЕФШЁжЕЗЖЮЇЃЛ
ЃЈ3ЃЉЙ§дЕуOЕФСэвЛЬѕжБЯпlНЛЫЋЧњЯпy=![]() ЃЈkЃО0ЃЉгкPЁЂQСНЕуЃЈPЕудкЕквЛЯѓЯоЃЉЃЌШєгЩЕуAЁЂPЁЂBЁЂQЮЊЖЅЕузщГЩЕФЫФБпаЮУцЛ§ЮЊ224ЃЌЧѓЕуPЕФзјБъЃЎ
ЃЈkЃО0ЃЉгкPЁЂQСНЕуЃЈPЕудкЕквЛЯѓЯоЃЉЃЌШєгЩЕуAЁЂPЁЂBЁЂQЮЊЖЅЕузщГЩЕФЫФБпаЮУцЛ§ЮЊ224ЃЌЧѓЕуPЕФзјБъЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌОиаЮ![]() ЕФЖдНЧЯп
ЕФЖдНЧЯп![]() ОЙ§ЕФзјБъдЕуЃЌОиаЮЕФБпЗжБ№ЦНаагкзјБъжсЃЌЕу
ОЙ§ЕФзјБъдЕуЃЌОиаЮЕФБпЗжБ№ЦНаагкзјБъжсЃЌЕу![]() дкЗДБШР§КЏЪ§
дкЗДБШР§КЏЪ§![]() ЕФЭМЯѓЩЯЃЌШєЕу
ЕФЭМЯѓЩЯЃЌШєЕу![]() ЕФзјБъЮЊ
ЕФзјБъЮЊ![]() ЃЌдђ
ЃЌдђ![]() ЕФжЕЮЊ________ЃЎ
ЕФжЕЮЊ________ЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌЗХжУЕФЁїOAB![]() ,Ёї
,Ёї![]() ,Ёї
,Ёї![]() ,ЁЖМЪЧБпГЄЮЊ2ЕФЕШБпШ§НЧаЮЃЌБпAOдк
,ЁЖМЪЧБпГЄЮЊ2ЕФЕШБпШ§НЧаЮЃЌБпAOдк![]() жсЩЯЃЌЕу
жсЩЯЃЌЕу![]() ЁЂ
ЁЂ![]() ЁЂ
ЁЂ![]() ЁЖМдкжБЯп
ЁЖМдкжБЯп![]() ЩЯЃЌдђЕу
ЩЯЃЌдђЕу![]() ЕФзјБъЮЊ_______
ЕФзјБъЮЊ_______

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌНЋ![]() ЗХдкУПИіаЁе§ЗНаЮЕФБпГЄЮЊ
ЗХдкУПИіаЁе§ЗНаЮЕФБпГЄЮЊ![]() ЕФЭјИёжаЃЌЕу
ЕФЭјИёжаЃЌЕу![]() ЁЂ
ЁЂ![]() ЁЂ
ЁЂ![]() ОљТфдкИёЕуЩЯЃЎ
ОљТфдкИёЕуЩЯЃЎ
ЃЈ1ЃЉ![]() ЕФУцЛ§ЕШгк________ЃЛ
ЕФУцЛ§ЕШгк________ЃЛ
![]() ШєЫФБпаЮ
ШєЫФБпаЮ![]() ЪЧ
ЪЧ![]() жаЫљФмАќКЌЕФУцЛ§зюДѓЕФе§ЗНаЮЃЌЧыФудкШчЭМЫљЪОЕФЭјИёжаЃЌгУжБГпКЭШ§НЧГпЛГіИУе§ЗНаЮЃЌВЂМђвЊЫЕУїЛЭМЗНЗЈЃЈВЛвЊЧѓжЄУїЃЉ________ЃЎ
жаЫљФмАќКЌЕФУцЛ§зюДѓЕФе§ЗНаЮЃЌЧыФудкШчЭМЫљЪОЕФЭјИёжаЃЌгУжБГпКЭШ§НЧГпЛГіИУе§ЗНаЮЃЌВЂМђвЊЫЕУїЛЭМЗНЗЈЃЈВЛвЊЧѓжЄУїЃЉ________ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
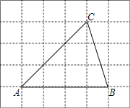
ЁОЬтФПЁПШчЭМЃЌдкЦНУцжБНЧзјБъЯЕжаЃЌжБЯпl1ЕФНтЮіЪНЮЊyЃНxЃЌжБЯпl2ЕФНтЮіЪНЮЊyЃНЃ![]() xЃЋ3ЃЌгыxжсЁЂyжсЗжБ№НЛгкЕуAЁЂЕуBЃЌжБЯпl1гыl2НЛгкЕуC.ЕуPЪЧyжсЩЯвЛЕу.
xЃЋ3ЃЌгыxжсЁЂyжсЗжБ№НЛгкЕуAЁЂЕуBЃЌжБЯпl1гыl2НЛгкЕуC.ЕуPЪЧyжсЩЯвЛЕу.

(1)аДГіЯТСаИїЕуЕФзјБъЃКЕуA( ЃЌ )ЁЂЕуB( ЃЌ )ЁЂЕуC( ЃЌ )ЃЛ
(2)ШєSЁїCOPЃНSЁїCOA,ЧыЧѓГіЕуPЕФзјБъЃЛ
(3)ЕБPAЃЋPCзюЖЬЪБЃЌЧѓГіжБЯпPCЕФНтЮіЪН.
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com