
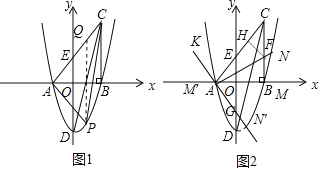
【题目】如图,在平面直角坐标系中,△ABC的一边AB在x轴上,∠ABC=90°,点C(4,8)在第一象限内,AC与y轴交于点E,抛物线y=![]() +bx+c经过A、B两点,与y轴交于点D(0,﹣6).
+bx+c经过A、B两点,与y轴交于点D(0,﹣6).

(1)请直接写出抛物线的表达式;
(2)求ED的长;
(3)点P是x轴下方抛物线上一动点,设点P的横坐标为m,△PAC的面积为S,试求出S与m的函数关系式;
(4)若点M是x轴上一点(不与点A重合),抛物线上是否存在点N,使∠CAN=∠MAN.若存在,请直接写出点N的坐标;若不存在,请说明理由.
【答案】(1)y=![]() ;(2)
;(2)![]() ;(3)S=﹣
;(3)S=﹣![]() m2+
m2+![]() m+26(﹣2<m<4);(4)(
m+26(﹣2<m<4);(4)(![]() ,
,![]() );(
);(![]() ,﹣
,﹣![]() )
)
【解析】
(1)先确定B(4,0),再利用待定系数法求出抛物线解析式为y=![]() ;
;
(2)先利用待定系数法求得直线AC的解析式为y=![]() x+
x+![]() ,则可确定E(0,
,则可确定E(0,![]() ),然后计算DE的长;
),然后计算DE的长;
(3)如图1,作PQ∥y轴交AC于Q,设P(m,![]() m2-
m2-![]() m-6),则Q(m,
m-6),则Q(m,![]() m+
m+![]() ),则PQ=-
),则PQ=-![]() m2+
m2+![]() m+
m+![]() ,然后根据三角形面积公式,利用S=S△PAQ+S△PCQ计算即可;
,然后根据三角形面积公式,利用S=S△PAQ+S△PCQ计算即可;
(4)如图2,当点M在x的正半轴,AN交BC于F,作FH⊥AC于H,根据角平分线的性质得FH=FB,易得AH=AB=6,再利用∠ACB的余弦可求出CF=5,则F(4,3),接着求出直线AF的解析式为y=![]() x+1,于是通过解方程组
x+1,于是通过解方程组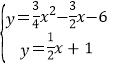 得N点坐标为(
得N点坐标为(![]() ,
,![]() );当点M′在x的负半轴上时,AN′交y轴与G,先在证明∴Rt△OAG∽Rt△BFA,在利用相似比求出OG=4,所以G(0,-4),接下来利用待定系数法求出直线AG的解析式为y=-2x-4,然后解方程组
);当点M′在x的负半轴上时,AN′交y轴与G,先在证明∴Rt△OAG∽Rt△BFA,在利用相似比求出OG=4,所以G(0,-4),接下来利用待定系数法求出直线AG的解析式为y=-2x-4,然后解方程组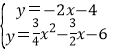 得N′的坐标.
得N′的坐标.
(1)∵BC⊥x轴,点C(4,8),
∴B(4,0),
把B(4,0),C(0,-6)代入y=![]() x2+bx+c得
x2+bx+c得
![]() ,解得
,解得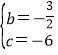 ,
,
∴抛物线解析式为y=![]() x2-
x2-![]() x-6;
x-6;
(2)设直线AC的解析式为y=px+q,
把A(-2,0),C(4,8)代入得
![]() ,解得
,解得![]() ,
,
∴直线AC的解析式为y=![]() x+
x+![]() ,
,
当x=0时,y=![]() x+
x+![]() =
=![]() ,则E(0,
,则E(0,![]() ),
),
∴DE=![]() +6=
+6=![]() ;
;
(3)如图1,作PQ∥y轴交AC于Q,
设P(m,![]() m2-
m2-![]() m-6),则Q(m,
m-6),则Q(m,![]() m+
m+![]() ),
),
∴PQ=![]() m+
m+![]() -(
-(![]() m2-
m2-![]() m-6)=-
m-6)=-![]() m2+
m2+![]() m+
m+![]() ,
,
∴S=S△PAQ+S△PCQ=![]() ×6×PQ=-
×6×PQ=-![]() m2+
m2+![]() m+26(-2<m<4);
m+26(-2<m<4);
(4)如图2,当点M在x的正半轴,AN交BC于F,作FH⊥AC于H,则FH=FB,
易得AH=AB=6,
∵AC=![]() ,
,
∴CH=10-6=4,
∵cos∠ACB=![]() ,
,
∴CF=![]() =5,
=5,
∴F(4,3),
易得直线AF的解析式为y=![]() x+1,
x+1,
解方程组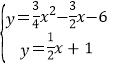 得
得![]() 或
或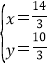 ,
,
∴N点坐标为(![]() ,
,![]() );
);
当点M′在x的负半轴上时,AN′交y轴与G,
∵∠CAN′=∠M′AN′,
∴∠KAM′=∠CAK,
而∠CAN=∠MAN,
∴∠KAC+∠CAN=90°,
而∠MAN+∠AFB=90°,
∴∠KAC=∠AFB,
而∠KAM′=∠GAO,
∴∠GAO=∠AFB,
∴Rt△OAG∽Rt△BFA,
∴![]() ,即
,即![]() ,解得OG=4,
,解得OG=4,
∴G(0,-4),
易得直线AG的解析式为y=-2x-4,
解方程组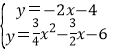 得
得![]() 或
或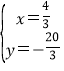 ,
,
∴N′的坐标为(![]() ,-
,-![]() ).
).
综上所述,满足条件的N点坐标为(![]() ,
,![]() ), (
), (![]() ,-
,-![]() ).
).


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】已知如图,在射线AB上依次作正方形A1B1B2C1、正方形A2B2B3C2、正方形A3B3B4C3…,点A1,A2,A3,…在射线OA上,点B1,B2,B3,…在射线OB上,若AB1=A1B1=1,则正方形AnBnBn+1Cn的边长为 _______.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,Rt△ABC的顶点C在第一象限,顶点A、B的坐标分别为(1,0),(4,0),∠CAB=90°,BC=5.抛物线y=![]() +bx+c与边AC,y轴的交点的纵坐标分别为3,
+bx+c与边AC,y轴的交点的纵坐标分别为3,![]() .
.
(1)求抛物线y=![]() +bx+c对应的函数关系式;
+bx+c对应的函数关系式;
(2)若将抛物线y=![]() +bx+c经过平移后的抛物线的顶点是边BC的中点,写出平移过程;
+bx+c经过平移后的抛物线的顶点是边BC的中点,写出平移过程;
(3)若抛物线y=![]() +bx+c平移后得到的抛物线y=
+bx+c平移后得到的抛物线y=![]() +k经过(﹣5,y1),(3,y2)两点,当y1>y2>k时,直接写出h的取值范围.
+k经过(﹣5,y1),(3,y2)两点,当y1>y2>k时,直接写出h的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,△ABD,△ACE都是等边三角形,
(1)求证:△ABE≌△ADC;
(2)若∠ACD=15°,求∠AEB的度数;
(3)如图2,当△ABD与△ACE的位置发生变化,使C、E、D三点在一条直线上,求证:AC∥BE.

查看答案和解析>>
科目:初中数学 来源: 题型:
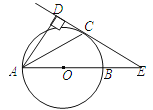
【题目】如图,已知AB是⊙O的直径,锐角∠DAB的平分线AC交⊙O于点C,作CD⊥AD,垂足为D,直线CD与AB的延长线交于点E.
(1)求证:直线CD为⊙O的切线;
(2)当AB=2BE,且CE=时,求AD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图![]() ,
,![]() 中,
中,![]() ,点
,点![]() 在
在![]() 的延长线上,点
的延长线上,点![]() 在
在![]() 上,
上,![]() ,点
,点![]() 是
是![]() 与
与![]() 的交点,且
的交点,且![]() .
.

![]() 图
图![]() 中是否存在与
中是否存在与![]() 相等的角?若存在,请找出,并加以证明,若不存在,说明理由;
相等的角?若存在,请找出,并加以证明,若不存在,说明理由;
![]() 求证:
求证:![]() ;
;
![]() 若将“点
若将“点![]() 在
在![]() 的延长线上,点
的延长线上,点![]() 在
在![]() 上”和“点
上”和“点![]() 是
是![]() 与
与![]() 的交点,且
的交点,且![]() ”分别改为“点
”分别改为“点![]() 在
在![]() 上,点
上,点![]() 在
在![]() 的延长线上”和“点
的延长线上”和“点![]() 是
是![]() 的延长线与
的延长线与![]() 的交点,且
的交点,且![]() ”,其他条件不变(如图
”,其他条件不变(如图![]() ).当
).当![]() ,
,![]() 时,求
时,求![]() 的长(用含
的长(用含![]() 、
、![]() 的式子表示).
的式子表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)已知:如图1,点A、D、C、B在同一条直线上,AD=BC,AE=BF,CE=DF,求证:AE∥BF.
(2)如图2所示,△ABC的顶点分别为A(﹣4,5),B(﹣3,2),C(4,﹣1)
①作出△ABC关于x轴对称的图形△A1B1C1;
②用三角板作出△ABC的AB边上的高CH.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com