
【题目】如图![]() ,
,![]() 中,
中,![]() ,点
,点![]() 在
在![]() 的延长线上,点
的延长线上,点![]() 在
在![]() 上,
上,![]() ,点
,点![]() 是
是![]() 与
与![]() 的交点,且
的交点,且![]() .
.

![]() 图
图![]() 中是否存在与
中是否存在与![]() 相等的角?若存在,请找出,并加以证明,若不存在,说明理由;
相等的角?若存在,请找出,并加以证明,若不存在,说明理由;
![]() 求证:
求证:![]() ;
;
![]() 若将“点
若将“点![]() 在
在![]() 的延长线上,点
的延长线上,点![]() 在
在![]() 上”和“点
上”和“点![]() 是
是![]() 与
与![]() 的交点,且
的交点,且![]() ”分别改为“点
”分别改为“点![]() 在
在![]() 上,点
上,点![]() 在
在![]() 的延长线上”和“点
的延长线上”和“点![]() 是
是![]() 的延长线与
的延长线与![]() 的交点,且
的交点,且![]() ”,其他条件不变(如图
”,其他条件不变(如图![]() ).当
).当![]() ,
,![]() 时,求
时,求![]() 的长(用含
的长(用含![]() 、
、![]() 的式子表示).
的式子表示).
【答案】![]() .
.![]() 证明见解析
证明见解析![]()
![]() 的长为
的长为![]() .
.
【解析】
(1)运用等腰三角形的性质及三角形的外角性质就可解决问题.
(2)过点E作EG∥AC,交AB于点G,如图1,要证BE=CE,只需证BG=AG,由DF=FE可证到DA=AG,只需证到DA=BG即DG=AB,也即DG=AC即可.只需证明△DCA≌△△EDG即可解决问题.
(3)过点A作AH⊥BC,垂足为H,如图2,可求出BC=2cosα.过点E作EG∥AC,交AB的延长线于点G,易证△DCA≌△△EDG,则有DA=EG,CA=DG=1.易证△ADF∽△GDE,则有![]() .由DF=kFE可得DE=EF-DF=(1-k)EF.从而可以求得AD=
.由DF=kFE可得DE=EF-DF=(1-k)EF.从而可以求得AD=![]() ,即GE=
,即GE=![]() .易证△ABC∽△GBE,则有
.易证△ABC∽△GBE,则有![]() ,从而可以求出BE.
,从而可以求出BE.
![]() .
.
证明:∵![]() ,
,![]() ,
,
∴![]() ,
,![]() .
.
∴![]() .
.![]() 过点
过点![]() 作
作![]() ,交
,交![]() 于点
于点![]() ,如图
,如图![]() ,
,
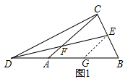
则有![]() .
.
在![]() 和
和![]() 中,
中,
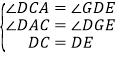
∴![]() .
.
∴![]() ,
,![]() .
.
∴![]() .
.
∴![]() .
.
∵![]() ,
,![]() ,
,
∴![]() .
.
∴![]() .
.
∵![]() ,
,
∴![]() .
.![]() 过点
过点![]() 作
作![]() ,交
,交![]() 的延长线于点
的延长线于点![]() ,如图
,如图![]() ,
,
∵![]() ,
,![]() ,
,
∴![]() ,
,![]() .
.
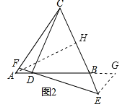
∴![]() .
.
∵![]() ,
,
∴![]() .
.
在![]() 和
和![]() 中,
中,
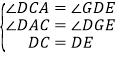
∴![]() .
.
∴![]() ,
,![]()
∴![]() .
.
∵![]() ,
,
∴![]() .
.
∴![]() .
.
∵![]() ,
,
∴![]() .
.
∴![]() .
.
∴![]() .
.
∴![]() .
.
过点![]() 作
作![]() ,垂足为
,垂足为![]() ,如图
,如图![]() ,
,
∵![]() ,
,![]() ,
,
∴![]() .
.
∴![]() .
.
∵![]() ,
,![]() ,
,
∴![]() .
.
∴![]() .
.
∵![]() ,
,
∴![]() .
.
∴![]() .
.
∴![]() .
.
∴![]() .
.
∴![]() 的长为
的长为![]() .
.


 小学能力测试卷系列答案
小学能力测试卷系列答案科目:初中数学 来源: 题型:
【题目】已知:如图,∠1=∠2,则不一定能使△ABD≌△ACD的条件是 ( )

A. AB=AC B. BD=CD C. ∠B=∠C D. ∠BDA=∠CDA
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,△ABC的一边AB在x轴上,∠ABC=90°,点C(4,8)在第一象限内,AC与y轴交于点E,抛物线y=![]() +bx+c经过A、B两点,与y轴交于点D(0,﹣6).
+bx+c经过A、B两点,与y轴交于点D(0,﹣6).

(1)请直接写出抛物线的表达式;
(2)求ED的长;
(3)点P是x轴下方抛物线上一动点,设点P的横坐标为m,△PAC的面积为S,试求出S与m的函数关系式;
(4)若点M是x轴上一点(不与点A重合),抛物线上是否存在点N,使∠CAN=∠MAN.若存在,请直接写出点N的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1) 观察被开方数a的小数点与算术平方根![]() 的小数点的移动规律:
的小数点的移动规律:
a | 0.0001 | 0.01 | 1 | 100 | 10000 |
| 0.01 | x | 1 | y | 100 |
填空:x= _______, y=______.
(2)根据你发现的规律填空:
①已知![]() ≈1.414,则
≈1.414,则![]() =________,
=________,![]() =_______;
=_______;
②![]() = 0.274,记
= 0.274,记![]() 的整数部分为x,则
的整数部分为x,则![]() =___________.
=___________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,对于平面直角坐标系x O y中的点A和点P,若将点P绕点A顺时针旋转90°后得到点Q,则称点Q为点P关于点A的“垂链点”.


(1) △PAQ是__________三角形;
(2)已知点A的坐标为(0, 0),点P关于点A的“垂链点”为点Q
①若点P的坐标为(2, 0),则点Q的坐标为___________;
②若点Q的坐标为(-2, 1),则点P的坐标为___________;
(3)如图2, 已知点D的坐标为(3, 0),点C在直线y=2x上,若点C关于点D的“垂链点”在坐标轴上,试求点C的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在线段BE上取一点C,分别以CB,CE为腰作等腰直角△BCA和等腰直角△DCE,连接BD和AE.

(1)请判断线段BD和线段AE的数量关系,并说明理由;
(2)如图2,若B,C,E三点不共线,(1)中的结论还成立吗?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】莆田元宵节从农历正月初六持续到正月廿九,堪称全国最长的元宵节,其中江东桔塔和延宁蔗塔十分引人关注.元宵节前夕,江东村和延宁村置办元宵节所需的桔子和甘蔗中,桔子重量比甘蔗重量少100千克.若市场上每千克桔子的价格是甘蔗的1.5倍,所采购桔子和甘蔗的费用都是1200元,求每千克桔子和甘蔗分别是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】图中是抛物线形拱桥,点P处有一照明灯,水面OA宽4 m,以O为原点,OA所在直线为x轴建立平面直角坐标系,已知点P的坐标为(3,![]() ).
).
(1)点P与水面的距离是________m;
(2)求这条抛物线的表达式;
(3)当水面上升1 m后,水面的宽变为多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知一次函数y=﹣![]() x+b的图象过点A(0,3),点p是该直线上的一个动点,过点P分别作PM垂直x轴于点M,PN垂直y轴于点N,在四边形PMON上分别截取:PC=
x+b的图象过点A(0,3),点p是该直线上的一个动点,过点P分别作PM垂直x轴于点M,PN垂直y轴于点N,在四边形PMON上分别截取:PC=![]() MP,MB=
MP,MB=![]() OM,OE=
OM,OE=![]() ON,ND=
ON,ND=![]() NP.
NP.
(1)b= ;
(2)求证:四边形BCDE是平行四边形;
(3)在直线y=﹣![]() x+b上是否存在这样的点P,使四边形BCDE为正方形?若存在,请求出所有符合的点P的坐标;若不存在,请说明理由.
x+b上是否存在这样的点P,使四边形BCDE为正方形?若存在,请求出所有符合的点P的坐标;若不存在,请说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com