【题目】如图，矩形ABCD中，E为BC上一点，DF⊥AE于F.
（1）ΔABE与ΔDFA相似吗？请说明理由；
（2）若AB=3，AD=6，BE=4，求DF的长.
【答案】(1)详见解析；（2）3.6.
【解析】
（1）由四边形ABCD是矩形结合DF⊥AE于点F易得：∠B=∠DFA=90°，∠AEB=∠DAF，从而可得△ABE∽△DFA；
（2）在△ABE中，由AB=3，BE=4，∠B=90°可得AE=5，由（1）中所得△ABE∽△DFA可得
，结合AD=6即可求得DF的长.
(1) ΔABE与ΔDFA相似，理由如下：
∵四边形ABCD是矩形，
∴AD//BC ，∠B=90°，
∴∠DAE=∠AEB，
∵DF⊥AE ，
∴∠B=∠AFD=90°，
∴△ABE∽△DFA ；
(2)在Rt△ABE中，∠B=90°，AB=3，BE=4，
∴AE=5，
∵△ABE∽△DFA，
∴ 
，
∴ 
，
∴DF=3.6.
第1卷单元月考期中期末系列答案科目：初中数学 来源： 题型：
【题目】如图：河上有一座抛物线形桥洞，已知桥下的水面离桥拱顶部3m时，水面宽AB＝6m，建立如图所示的坐标系．
（1）当水位上升0.5m时，求水面宽度CD为多少米？（结果可保留根号）
（2）有一艘游船它的左右两边缘最宽处有一个长方体形状的遮阳棚，此船正对着桥洞在上述河流中航行，若这船宽（最大宽度）2米，从水面到棚顶高度为1.8米．问这艘船能否从桥下洞通过？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】综合与探究
如图，抛物线y＝﹣
x2﹣
x+
与x轴交于A、B两点（点A在点B的左侧），与y轴交于点C，直线l经过B、C两点，点M从点A出发以每秒1个单位长度的速度向终点B运动，连接CM，将线段MC绕点M顺时针旋转90°得到线段MD，连接CD、BD．设点M运动的时间为t（t＞0），请解答下列问题：
（1）求点A的坐标与直线l的表达式；
（2）①请直接写出点D的坐标（用含t的式子表示），并求点D落在直线l上时t的值；
②求点M运动的过程中线段CD长度的最小值．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知在平面直角坐标系xOy中（如图），抛物线y=ax2-4与x轴的负半轴相交于点A，与y轴相交于点B，AB=2
.点P在抛物线上，线段AP与y轴的正半轴交于点C，线段BP与x轴相交于点D，设点P的横坐标为m.
（1）求这条抛物线的解析式；
（2）用含m的代数式表示线段CO的长；
（3）当tan∠ODC=
时，求∠PAD的正弦值.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知抛物线
（其中
、
为常数且
）与
轴交于
和
两点，与
轴交于点
.
（1）当
时，求抛物线的对称轴方程及顶点坐标；
（2）填空：
__________，点的坐标为____________.（以上结果均用含的式子表示）；
（3）连接
，线段的垂直平分线交抛物线的对称轴于点
，轴上存在一点
（异于点）使得
.
①求点的坐标；
②点关于抛物线对称轴的对称点为点
，试求
面积的最大值.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图是一个半圆形桥洞截面示意图，圆心为O，直径AB是河底线，弦CD是水位线，CD∥AB，且AB=26m，OE⊥CD于点E．水位正常时测得OE∶CD=5∶24
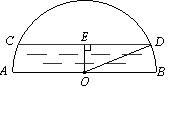
（1）求CD的长；
（2）现汛期来临，水面要以每小时4 m的速度上升，则经过多长时间桥洞会刚刚被灌满？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】关于x的一元二次方程x2﹣（m﹣3）x﹣m2=0．
（1）证明：方程总有两个不相等的实数根；
（2）设这个方程的两个实数根为x1，x2，且|x1|=|x2|﹣2，求m的值及方程的根．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知抛物线经过E(4，5)，F（2，－3），G（－2，5），H（1，－4）四个点，选取其中两点用待定系数法能求出该抛物线解析式的是（ ）
A.E，FB.F，GC.F，HD.E，G
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在ABCD中 过点A作AE⊥DC，垂足为E，连接BE，F为BE上一点，且∠AFE=∠D．
（1）求证：△ABF∽△BEC；
（2）若AD=5，AB=8，sinD=
，求AF的长．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com