
����Ŀ���ۺ���̽��
��ͼ��������y����![]() x2��
x2��![]() x+
x+![]() ��x�ύ��A��B���㣨��A�ڵ�B����ࣩ����y�ύ�ڵ�C��ֱ��l����B��C���㣬��M�ӵ�A������ÿ��1����λ���ȵ��ٶ����յ�B�˶�������CM�����߶�MC�Ƶ�M˳ʱ����ת90���õ��߶�MD������CD��BD�����M�˶���ʱ��Ϊt��t��0���������������⣺
��x�ύ��A��B���㣨��A�ڵ�B����ࣩ����y�ύ�ڵ�C��ֱ��l����B��C���㣬��M�ӵ�A������ÿ��1����λ���ȵ��ٶ����յ�B�˶�������CM�����߶�MC�Ƶ�M˳ʱ����ת90���õ��߶�MD������CD��BD�����M�˶���ʱ��Ϊt��t��0���������������⣺

��1�����A��������ֱ��l�ı���ʽ��
��2������ֱ��д����D�����꣨�ú�t��ʽ�ӱ�ʾ���������D����ֱ��l��ʱt��ֵ��
�����M�˶��Ĺ������߶�CD���ȵ���Сֵ��
���𰸡���1��A����3��0����y����![]() x+
x+![]() ����2���ٵ�D����ֱ��l��ʱ��t��6��2
����2���ٵ�D����ֱ��l��ʱ��t��6��2![]() ����CD����СֵΪ
����CD����СֵΪ![]() ��
��
��������
��1���ⷽ�������A����B�����꣬���ݶ��κ��������������C�����꣬���ô���ϵ�������ֱ��l�ı���ʽ��
��2�����ֵ�M��AO���˶�����M��OB���˶����������DN��x����N��֤����MCO�ա�DMN������ȫ�������ε����ʵõ�MN��OC��![]() ��DN��OM��3��t���õ���D�����꣬����һ�κ���ͼ���ϵ�������������t��
��DN��OM��3��t���õ���D�����꣬����һ�κ���ͼ���ϵ�������������t��
�����ݵ���ֱ�������ε����ʡ����߶���̽��
��1����y��0ʱ����![]() x2��
x2��![]() x+
x+![]() =0��
=0��
���x1��1��x2����3��
����A�ڵ�B����࣬
��A����3��0����B��1��0����
��x��0ʱ��y��![]() ����C��0��
����C��0��![]() ����
����
��ֱ��l�ı���ʽΪy��kx+b��
��B��C�����������ã�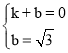 ��
��
��ã�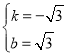 ��
��
��ֱ��l�ı���ʽΪy����![]() x+
x+![]() ��
��
��2������ͼ1������M��AO���˶�ʱ������D��DN��x����N��
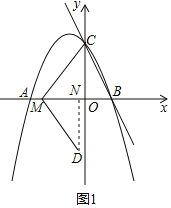
�������֪��AM��t��OM��3��t��MC��MD��
����DMN+��CMO��90������CMO+��MCO��90����
���MCO����DMN��
����MCO����DMN��
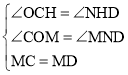 ��
��
���MCO�ա�DMN��AAS����
��MN��OC��![]() ��DN��OM��3��t��
��DN��OM��3��t��
��D��t��3+![]() ��t��3����
��t��3����
ͬ������ͼ2������M��OB���˶�ʱ��
��D��������D����3+t+![]() ��t��3��
��t��3��
��D���������ֱ��BC�Ľ���ʽy����![]() x+
x+![]() �ã�t��3����
�ã�t��3����![]() ������3+t+
������3+t+![]() ��+
��+![]() ��
��
t��6��2![]() ������D����ֱ��l��ʱ��t��6��2
������D����ֱ��l��ʱ��t��6��2![]() ��
��
�ڡߡ�COD�ǵ���ֱ�������Σ�
��CM��MD��
���߶�CM��Сʱ���߶�CD���ȵ���С��
��M��AB���˶���
����CM��ABʱ��CM��̣�CD��̣���CM��CO��![]() ��
��
���ݹ��ɶ����ã�CD����СֵΪ![]() ��
��
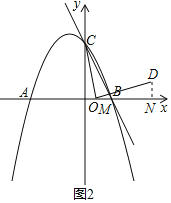


 ��1����Ԫ�¿�������ĩϵ�д�
��1����Ԫ�¿�������ĩϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
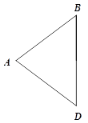
����Ŀ����ͼ������ABD�У���ABD = ��ADB���ֱ��Ե�B��DΪԲ�ģ�AB��Ϊ�뾶��BD���Ҳ��������������ڵ�C������BC��DC��AC��AC��BD���ڵ�O��
��1���ó߹油ȫͼ�Σ���֤���ı���ABCDΪ���Σ�
��2�����AB = 5��![]() ����BD�ij���
����BD�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����κ���![]() ��
��![]() �dz�����
�dz�����![]() �����Ա���
�����Ա���![]() �뺯��ֵ
�뺯��ֵ![]() �IJ��ֶ�Ӧֵ���±���
�IJ��ֶ�Ӧֵ���±���
| �� |
|
| 0 | 1 | 2 | �� |
| �� |
|
|
|
|
| �� |
�ҵ�![]() ʱ�������Ӧ�ĺ���ֵ
ʱ�������Ӧ�ĺ���ֵ![]() �������н��ۣ���
�������н��ۣ���![]() ����
����![]() ��3�ǹ���
��3�ǹ���![]() �ķ���
�ķ���![]() ������������
������������![]()
![]() �����У���ȷ���۵ĸ����ǣ� ��
�����У���ȷ���۵ĸ����ǣ� ��
A. 0B. 1C. 2D. 3
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����κ���y = ![]() ax2 ax + cͼ��Ķ���ΪC��һ�κ���y = x + 3��ͼ����������κ�����ͼ����A��B����(���е�A�ڵ�B�����)�������ĶԳ��ύ�ڵ�D��
ax2 ax + cͼ��Ķ���ΪC��һ�κ���y = x + 3��ͼ����������κ�����ͼ����A��B����(���е�A�ڵ�B�����)�������ĶԳ��ύ�ڵ�D��
(1)���D�����ꣻ
(2) ������C���D����x��Գƣ��ҡ�BCD���������4����˶��κ����Ĺ�ϵʽ��
����CD=DB���ҡ�BCD���������4![]() ����a��ֵ��
����a��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
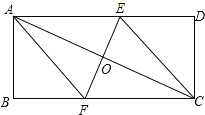
����Ŀ����ͼ������ABCD�ĶԽ���AC�Ĵ�ֱƽ����EF��AD��AC��BC�ֱ��ڵ�E��O��F��
��1����֤���ı���AFCE�����Σ�
��2����AB��5��BC��12��������AFCE�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
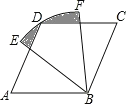
����Ŀ����ͼ���ı���ABCD�����Σ���A��60����AB��2������EBF�İ뾶Ϊ2��Բ�Ľ�Ϊ60������ͼ����Ӱ���ֵ������_____��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���л��Ļ���ԴԶ����������ѧ���棬�����μǡ������������塷����ˮ䰴���������¥�Ρ����ҹ��Ŵ���ƪС˵�еĵ��ʹ���������Ϊ���Ĵ�ŵ���������ij��ѧΪ���˽�ѧ�����Ĵ�ŵ��������Ķ�������͡��Ĵ�ŵ�����������˼���������������ȫУѧ���н����˳������飬���ݵ��������Ƴ���ͼ��ʾ��������������ͳ��ͼ������ͼ����Ϣ����������⣺
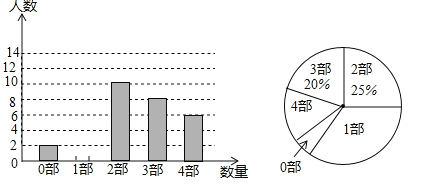
��1�����ε����������ݵ������� ������λ���� ��������ͳ��ͼ�С�1�����������ε�Բ�Ľ�Ϊ �ȣ�
��2���뽫����ͳ��ͼ����������
��3��û�ж����Ĵ�ŵ�����������ѧ�������Ĵ�̶������и������ѡ��һ�����Ķ���������ѡ��ͬһ�����ĸ���Ϊ ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
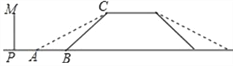
����Ŀ��ij�ص�һ������������ͼ��ʾ�����Ÿ�Ϊ6�ף�����BC���¶�Ϊ1��1��Ϊ�˷��������Ƴ������ţ��йز��ž��������¶ȣ�ʹ��������¶�Ϊ1��![]() ��
��
��1������������½ǡ�CAB�Ķ�����
��2��ԭ���ŵײ���ǰ��8�״���PB�ij������Ļ�ǽPM�Ƿ���Ҫ�������˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������С������Ƶ�����һ����30���ǵ�ֱ�����������ij߹���ͼ���̣�
��֪��ֱ��l��
![]()
��������ABC��ʹ�á�ACB��90������ABC��30����
��������ͼ��
![]()
����ֱ��l����ȡ����O��A��
���Ե�OΪԲ�ģ�OA��Ϊ�뾶��������ֱ��l�ڵ�B��
���Ե�AΪԲ�ģ�AO��Ϊ�뾶��������![]() �ڵ�C��
�ڵ�C��
������AC��BC��
������ABC������������������
����С����Ƶij߹���ͼ���̣�
��1��ʹ��ֱ�ߺ�Բ�棬��ȫͼ�Σ���������ͼ�ۼ���
��2����������֤����
֤�����ڡ�O�У�ABΪֱ����
���ACB��90������ �������������������ݣ�
����OC
��OA��OC��AC��
���CAB��60����
���ABC��30�������� �������������������ݣ�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com