
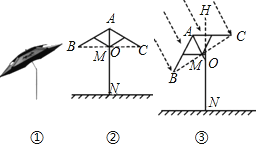
【题目】如图①是钓鱼伞,为遮挡不同方向的阳光,钓鱼伞可以在撑杆AN上的点O处弯折并旋转任意角,图②是钓鱼伞直立时的示意图,当伞完全撑开时,伞骨AB,AC与水平方向的夹角∠ABC=∠ACB=30°,伞骨AB与AC水平方向的最大距离BC=2m,BC与AN交于点M,撑杆AN=2.2m,固定点O到地面的距离ON=1.6m.
(1)如图②,当伞完全撑开并直立时,求点B到地面的距离.
(2)某日某时,为了增加遮挡斜射阳光的面积,将钓鱼伞倾斜与铅垂线HN成30°夹角,如图③.
①求此时点B到地面的距离;
②若斜射阳光与BC所在直线垂直时,求BC在水平地面上投影的长度约是多少.(说明:![]() ≈1.732,结果精确到0.1m)
≈1.732,结果精确到0.1m)
【答案】(1)点B到地面的距离约为1.6 m;(2)①此时点B到地面的距离约为1.1 m;②BC在水平地面上投影的长度约为2.3 m.
【解析】
(1)求出AM的长即可得出答案;
(2)①过点A,B分别作地面的垂线,垂足分别为Q,T,求出∠ABS=30°,则BS=BM=1.可得BT=OP+ON﹣SB,求出答案;②可知BC⊥CD,∠CBD=30°.可求出BD的长.
解:(1)点B到地面的距离即为MN的长度,
MN=AN﹣AM=AN﹣BMtan30°=2.2﹣![]() ≈1.6(m).
≈1.6(m).
答:点B到地面的距离约为1.6 m.
(2)①如图①,过点A,B分别作地面的垂线,垂足分别为Q,T,
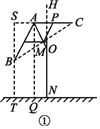
∵∠AOH=30°,
∴∠OAQ=30°.
∵∠ABC=30°,
∴∠BAO=90°﹣∠ABC=60°,
∴∠BAQ=∠BAO﹣∠OAQ=30°,
∴∠ABS=30°,
∴BS=BM=1.
∴BT=OP+ON﹣SB=OAcos30°+ON﹣SB=0.6×![]() +1.6﹣1≈1.1(m).
+1.6﹣1≈1.1(m).
答:此时点B到地面的距离约为1.1 m.
②如图②,依题意,可知BC⊥CD,∠CBD=30°.
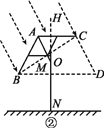
∵BC=2,
∴BD=![]() ≈2.3(m).
≈2.3(m).
答:BC在水平地面上投影的长度约为2.3 m.


 百年学典课时学练测系列答案
百年学典课时学练测系列答案科目:初中数学 来源: 题型:
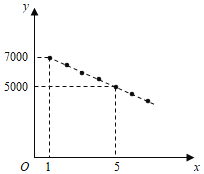
【题目】随着![]() 技术的发展,人们对各类
技术的发展,人们对各类![]() 产品的使用充满期待.某公司计划在某地区销售第一款
产品的使用充满期待.某公司计划在某地区销售第一款![]() 产品,根据市场分析,该产品的销售价格将随销售周期的变化而变化.设该产品在第
产品,根据市场分析,该产品的销售价格将随销售周期的变化而变化.设该产品在第![]() (
(![]() 为正整数)个销售周期每台的销售价格为
为正整数)个销售周期每台的销售价格为![]() 元,
元,![]() 与
与![]() 之间满足如图所示的一次函数关系.
之间满足如图所示的一次函数关系.
(1)求![]() 与
与![]() 之间的关系式;
之间的关系式;
(2)设该产品在第![]() 个销售周期的销售数量为
个销售周期的销售数量为![]() (万台),
(万台),![]() 与
与![]() 的关系可用
的关系可用![]() 来描述.根据以上信息,试问:哪个销售周期的销售收入最大?此时该产品每台的销售价格是多少元?
来描述.根据以上信息,试问:哪个销售周期的销售收入最大?此时该产品每台的销售价格是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于抛物线![]() ,下列说法错误的是( )
,下列说法错误的是( )
A.若顶点在x轴下方,则一元二次方程![]() 有两个不相等的实数根
有两个不相等的实数根
B.若抛物线经过原点,则一元二次方程![]() 必有一根为0
必有一根为0
C.若![]() ,则抛物线的对称轴必在y轴的左侧
,则抛物线的对称轴必在y轴的左侧
D.若![]() ,则一元二次方程
,则一元二次方程![]() ,必有一根为-2
,必有一根为-2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】三角板是我们学习数学的好帮手.将一对直角三角板如图放置,点C在FD的延长线上,点B在ED上,AB∥CF,∠F=∠ACB=90°,∠E=45°,∠A=60°,AC=10,则CD的长度是_____.
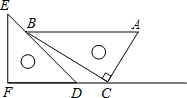
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 是
是![]() 的直径,弦
的直径,弦![]() 点
点![]() 是直径
是直径![]() 上方半圆上的动点(包括端点
上方半圆上的动点(包括端点![]() 和
和![]() 的平分线相交于点E,当点
的平分线相交于点E,当点![]() 从点
从点![]() 运动到点
运动到点![]() 时,则
时,则![]() 两点的运动路径长的比值是( )
两点的运动路径长的比值是( )
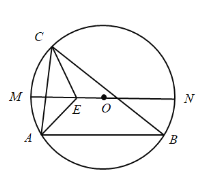
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,二次函数![]() 的图像与
的图像与![]() 轴交于
轴交于![]() 两点,与
两点,与![]() 轴交于点
轴交于点![]() .
.
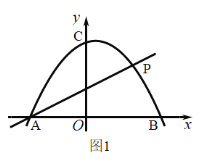
(1)求抛物线的函数关系式;
(2)点![]() 是抛物线第象限上一点,设点
是抛物线第象限上一点,设点![]() 的横坐标为
的横坐标为![]() ,连接
,连接![]() ,如果点
,如果点![]() 关于直线
关于直线![]() 的对称点
的对称点![]() 落在
落在![]() 轴下方(含
轴下方(含![]() 轴),求
轴),求![]() 的取值范围;
的取值范围;
(3)如图2,连接![]() 将
将![]() 绕平面内某点
绕平面内某点![]() 顺时针旋转
顺时针旋转![]() ,得到
,得到![]() 点
点![]() 的对应点分别是点
的对应点分别是点![]() 、若
、若![]() 的两个项点恰好落在抛物线上,请直接写出点
的两个项点恰好落在抛物线上,请直接写出点![]() 的坐标 .
的坐标 .
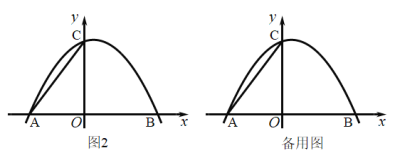
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个不透明的口袋中有标号为1,2,3,4的四个小球,除数字不同外,小球没有任何区别,摸球前先搅拌均匀,每次摸一个球
(1)摸出一个球,摸到标号为偶数的概率为 .
(2)从袋中不放回地摸两次,用列表或树状图求出两球标号数字为一奇一偶的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com