
【题目】如图1,二次函数![]() 的图像与
的图像与![]() 轴交于
轴交于![]() 两点,与
两点,与![]() 轴交于点
轴交于点![]() .
.
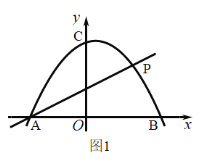
(1)求抛物线的函数关系式;
(2)点![]() 是抛物线第象限上一点,设点
是抛物线第象限上一点,设点![]() 的横坐标为
的横坐标为![]() ,连接
,连接![]() ,如果点
,如果点![]() 关于直线
关于直线![]() 的对称点
的对称点![]() 落在
落在![]() 轴下方(含
轴下方(含![]() 轴),求
轴),求![]() 的取值范围;
的取值范围;
(3)如图2,连接![]() 将
将![]() 绕平面内某点
绕平面内某点![]() 顺时针旋转
顺时针旋转![]() ,得到
,得到![]() 点
点![]() 的对应点分别是点
的对应点分别是点![]() 、若
、若![]() 的两个项点恰好落在抛物线上,请直接写出点
的两个项点恰好落在抛物线上,请直接写出点![]() 的坐标 .
的坐标 .
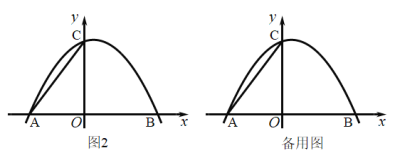
【答案】(1)![]() ;(2)
;(2)![]() 的取值范围为
的取值范围为![]() ; (3)点
; (3)点![]() 的坐标为
的坐标为![]() 或
或![]()
【解析】
(1)直接利用待定系数法即可求解;
(2)首先根据二次函数的解析式求出B,C的坐标,然后设点![]() 关于直线
关于直线![]() 对称的点恰好在
对称的点恰好在![]() 轴上时,对称点为
轴上时,对称点为![]() ,根据轴对称的性质和勾股定理求出点E的坐标,进而求出直线AP的解析式,然后将直线AP的解析式与二次函数的解析式联立,求出P点的横坐标,然后数形结合即可得出答案;
,根据轴对称的性质和勾股定理求出点E的坐标,进而求出直线AP的解析式,然后将直线AP的解析式与二次函数的解析式联立,求出P点的横坐标,然后数形结合即可得出答案;
(3)分两种情况:当![]() 在二次函数图像上时和当
在二次函数图像上时和当![]() 在二次函数图像上时,设点
在二次函数图像上时,设点![]() 的坐标为
的坐标为![]() 将点的坐标代入二次函数中,通过联立求方程组的解即可得出答案.
将点的坐标代入二次函数中,通过联立求方程组的解即可得出答案.
![]() 二次函数
二次函数![]() 的图象过点
的图象过点![]()
![]()
![]()
即![]() ;
;
![]() 令
令![]() ,则
,则![]()
解得![]() ,
,
![]() ,
,
令![]() ,则
,则![]()
![]() ,
,
则![]()
设点![]() 关于直线
关于直线![]() 对称的点恰好在
对称的点恰好在![]() 轴上时,对称点为
轴上时,对称点为![]() ,
,
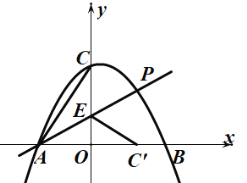
![]() ,
,
![]()
设![]() 长为
长为![]()
则![]()
在![]() 中,
中,![]() ,
,
即![]()
解得![]()
![]() 点
点![]() 的坐标为
的坐标为![]() ,
,
设直线![]() 的函数表达式为
的函数表达式为![]()
所以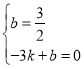 解得
解得![]()
即![]() .
.
设直线![]() 与二次函数的图像交点的横坐标为
与二次函数的图像交点的横坐标为![]() ,
,
则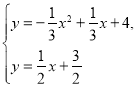
解得![]() ,
,
![]() 点
点![]() 关于直线
关于直线![]() 的对称点
的对称点![]() 落在
落在![]() 轴下方(含
轴下方(含![]() 轴)时,
轴)时,
![]() 的取值范围为
的取值范围为![]() ;
;
![]() 设点
设点![]() 的坐标为
的坐标为![]()
当![]() 在二次函数图像上时,
在二次函数图像上时,
则点![]() 的坐标为
的坐标为![]() 、点
、点![]() 的坐标为
的坐标为![]()
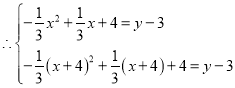
解得 ,
,
即点![]() 的坐标为
的坐标为![]() ;
;
当![]() 在二次函数图像上时,
在二次函数图像上时,
则点![]() 的坐标为
的坐标为![]()
 ,
,
解得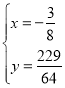
即点![]() 的坐标为
的坐标为![]()
综上可知点![]() 的坐标为
的坐标为![]() 或
或![]()


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】2018年非洲猪瘟疫情暴发后,今年猪肉价格不断走高,引起了民众与政府的高度关注,据统计:今年7月20日猪肉价格比今年年初上涨了60%,某市民今年7月20日在某超市购买1千克猪肉花了80元钱.
(1)问:今年年初猪肉的价格为每千克多少元?
(2)某超市将进货价为每千克65元的猪肉,按7月20日价格出售,平均一天能销售出100千克,经调查表明:猪肉的售价每千克下降1元,其日销售量就增加10千克,超市为了实现销售猪内每天有1560元的利润,并且可能让顾客得到实惠,猪肉的售价应该下降多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
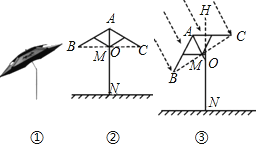
【题目】如图①是钓鱼伞,为遮挡不同方向的阳光,钓鱼伞可以在撑杆AN上的点O处弯折并旋转任意角,图②是钓鱼伞直立时的示意图,当伞完全撑开时,伞骨AB,AC与水平方向的夹角∠ABC=∠ACB=30°,伞骨AB与AC水平方向的最大距离BC=2m,BC与AN交于点M,撑杆AN=2.2m,固定点O到地面的距离ON=1.6m.
(1)如图②,当伞完全撑开并直立时,求点B到地面的距离.
(2)某日某时,为了增加遮挡斜射阳光的面积,将钓鱼伞倾斜与铅垂线HN成30°夹角,如图③.
①求此时点B到地面的距离;
②若斜射阳光与BC所在直线垂直时,求BC在水平地面上投影的长度约是多少.(说明:![]() ≈1.732,结果精确到0.1m)
≈1.732,结果精确到0.1m)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】疫情初期,某市出台《中小学教师志愿辅导工作实施意见》,鼓励教师参与志愿辅导,该市率先示范,推出名师公益课程,为学生提供线上免费辅导,据统计,第一批公益课受益学生![]() 万人次,第三批公益课受益人数
万人次,第三批公益课受益人数![]() 万人次.
万人次.
(1)如果第二批,第三批公益课受益学生人次的增长率相同,求这个增长率;
(2)按照这个增长率,预计第四批公益课受益学生将达到多少万人次?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市一研究机构为了了解![]() 岁年龄段市民对创建文明城市的关注程度,随机选取了
岁年龄段市民对创建文明城市的关注程度,随机选取了![]() 名年龄在该范围内的市民进行了调查,并将收集到的数据制成了尚不完整的频数分布表、频数分布直方图和扇形统计图,如下所示:
名年龄在该范围内的市民进行了调查,并将收集到的数据制成了尚不完整的频数分布表、频数分布直方图和扇形统计图,如下所示:
组别 | 年龄段 | 频数(人数) |
第 |
|
|
第 |
|
|
第 |
|
|
第 |
|
|
第 |
|
|
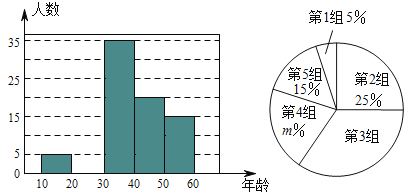
(1)请直接写出![]() ,第
,第![]() 组人数在扇形统计图中所对应的圆心角是 度;
组人数在扇形统计图中所对应的圆心角是 度;
(2)请补全上面的频数分布直方图:
(3)假设该市现有![]() 岁的市民
岁的市民![]() 万人,问
万人,问![]() 岁年龄段的关注创建文明城市的人数约有多少?
岁年龄段的关注创建文明城市的人数约有多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
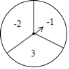
【题目】如图,可以自由转动的转盘被平均分成了三等分标有数字﹣2,3,﹣1的扇形区域转动转盘,待转盘自动停止后,指针指向一个扇形的内部,则该扇形内的数字即为转出的数字,此时,称为转动转盘一次(若指针指向两个扇形的交线,则不计转动的次数,重新转动转盘,直到指针指向一个扇形的内部为止)
(1)转动转盘一次,求转出的数字是3的概率;
(2)转动转盘两次,设第一次得到的数字为x,第二次得到的数字为y,点M的坐标为(x,y),请用树状图或列表法求点M在反比例函数y=﹣![]() 的图象上的概率.
的图象上的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】第5代移动通信技术简称5G,某地已开通5G业务,经测试5G下载速度是4G下载速度的15倍,小明和小强分别用5G与4G下载一部600兆的公益片,小明比小强所用的时间快140秒,求该地4G与5G的下载速度分别是每秒多少兆?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学开设的体育选修课有篮球、足球、排球、羽毛球、乒乓球,学生可以根据自己的爱好选修其中1门.某班班主任对全班同学的选课情况进行了调查统计,制成了两幅不完整的统计图(图(1)和图(2)):
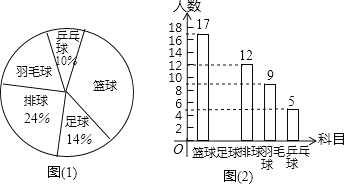
(1)请你求出该班的总人数,并补全条形图(注:在所补小矩形上方标出人数);
(2)在该班团支部4人中,有1人选修排球,2人选修羽毛球,1人选修乒乓球.如果该班班主任要从他们4人中任选2人作为学生会候选人,那么选出的两人中恰好有1人选修排球、1人选修羽毛球的概率是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com