
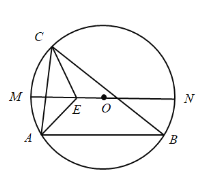
【题目】如图,![]() 是
是![]() 的直径,弦
的直径,弦![]() 点
点![]() 是直径
是直径![]() 上方半圆上的动点(包括端点
上方半圆上的动点(包括端点![]() 和
和![]() 的平分线相交于点E,当点
的平分线相交于点E,当点![]() 从点
从点![]() 运动到点
运动到点![]() 时,则
时,则![]() 两点的运动路径长的比值是( )
两点的运动路径长的比值是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】C
【解析】
延长![]() 交
交![]() 于点
于点![]() ,连接DA、DB,由圆周角定理和等角对等边的性质可知DA=DE,据此可知,
,连接DA、DB,由圆周角定理和等角对等边的性质可知DA=DE,据此可知,![]() 在以
在以![]() 为圆心,
为圆心,![]() 长为半径的圆上,根据角平分线的性质、圆周角定理及等边三角形的判定可知
长为半径的圆上,根据角平分线的性质、圆周角定理及等边三角形的判定可知![]() 为等边三角形,进而可知DA=DB=DO,由此可知,当
为等边三角形,进而可知DA=DB=DO,由此可知,当![]() 由
由![]() 运动到到
运动到到![]() 时,
时,![]() 运动路径为
运动路径为![]() ,
,![]() 运动路径为
运动路径为![]() ,与
,与![]() 对应的圆周半径相同,最后计算路径长度比即为圆心角之比.
对应的圆周半径相同,最后计算路径长度比即为圆心角之比.
如图1,延长![]() 交
交![]() 于点
于点![]() ,
,
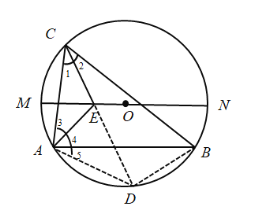
由![]() 平分
平分![]() 得
得![]() 恒为劣弧
恒为劣弧![]() 中点.
中点.
由已知,得![]() ,
,
则![]() ,
,
得![]() .
.
故![]() 在以
在以![]() 为圆心,
为圆心,![]() 长为半径的圆上.
长为半径的圆上.
∵∠ACB=2∠2=60°,
∴∠2=30°,
∴∠BOD=60°,
∵DO=BO,
∴△BOD是等边三角形,
∴DO=DB=DA,
如图2,当![]() 由
由![]() 运动到到
运动到到![]() 时,
时,![]() 运动轨迹为
运动轨迹为![]() .
.
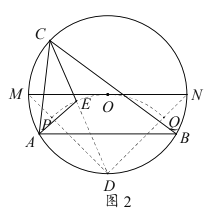
![]() 运动路径为
运动路径为![]() 与路径
与路径![]() 对应的圆周半径相同,计算路径长度比即为圆心角之比,
对应的圆周半径相同,计算路径长度比即为圆心角之比,
由![]() 得路径长度之比为
得路径长度之比为![]() .
.
故选:C.


 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案科目:初中数学 来源: 题型:
【题目】现有![]() ,
,![]() 两个不透明的袋子,分别装有3个除颜色外完全相同的小球.其中,
两个不透明的袋子,分别装有3个除颜色外完全相同的小球.其中,![]() 袋装有1个白球,2个红球;
袋装有1个白球,2个红球;![]() 袋装有1个红球,2个白球.
袋装有1个红球,2个白球.
(1)将![]() 袋摇匀,然后从
袋摇匀,然后从![]() 袋中随机摸出一个球,则摸出的小球是红球的概率为______;
袋中随机摸出一个球,则摸出的小球是红球的概率为______;
(2)小王和小周商定了一个游戏规则:从摇匀后的![]() ,
,![]() 两袋中各随机摸出一个球,摸出的这两个球,若颜色相同,则小王获胜;若颜色不同,则小周获胜.请利用概率说明这个游戏规则是否公平.
两袋中各随机摸出一个球,摸出的这两个球,若颜色相同,则小王获胜;若颜色不同,则小周获胜.请利用概率说明这个游戏规则是否公平.
查看答案和解析>>
科目:初中数学 来源: 题型:
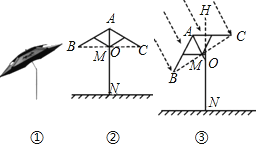
【题目】如图①是钓鱼伞,为遮挡不同方向的阳光,钓鱼伞可以在撑杆AN上的点O处弯折并旋转任意角,图②是钓鱼伞直立时的示意图,当伞完全撑开时,伞骨AB,AC与水平方向的夹角∠ABC=∠ACB=30°,伞骨AB与AC水平方向的最大距离BC=2m,BC与AN交于点M,撑杆AN=2.2m,固定点O到地面的距离ON=1.6m.
(1)如图②,当伞完全撑开并直立时,求点B到地面的距离.
(2)某日某时,为了增加遮挡斜射阳光的面积,将钓鱼伞倾斜与铅垂线HN成30°夹角,如图③.
①求此时点B到地面的距离;
②若斜射阳光与BC所在直线垂直时,求BC在水平地面上投影的长度约是多少.(说明:![]() ≈1.732,结果精确到0.1m)
≈1.732,结果精确到0.1m)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学数学兴趣小组在一次课外学习与探究中遇到一些新的数学符号,他们将其中某些材料摘录如下:
对于三个实数a,b,c,用M{a,b,c}表示这三个数的平均数,用min{a,b,c}表示这三个数中最小的数.例如:M{1,2,9}=![]() =4,min{1,2,﹣3}=﹣3,min{3,1,1}=1.请结合上述材料,解决下列问题:
=4,min{1,2,﹣3}=﹣3,min{3,1,1}=1.请结合上述材料,解决下列问题:
(1)①M{(﹣2)2,22,﹣22}= ; ②min{sin30°,cos60°,tan45°}= ;
(2)若M{﹣2x,x2,3}=2,求x的值;
(3)若min{3﹣2x,1+3x,﹣5}=﹣5,求x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】疫情初期,某市出台《中小学教师志愿辅导工作实施意见》,鼓励教师参与志愿辅导,该市率先示范,推出名师公益课程,为学生提供线上免费辅导,据统计,第一批公益课受益学生![]() 万人次,第三批公益课受益人数
万人次,第三批公益课受益人数![]() 万人次.
万人次.
(1)如果第二批,第三批公益课受益学生人次的增长率相同,求这个增长率;
(2)按照这个增长率,预计第四批公益课受益学生将达到多少万人次?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市一研究机构为了了解![]() 岁年龄段市民对创建文明城市的关注程度,随机选取了
岁年龄段市民对创建文明城市的关注程度,随机选取了![]() 名年龄在该范围内的市民进行了调查,并将收集到的数据制成了尚不完整的频数分布表、频数分布直方图和扇形统计图,如下所示:
名年龄在该范围内的市民进行了调查,并将收集到的数据制成了尚不完整的频数分布表、频数分布直方图和扇形统计图,如下所示:
组别 | 年龄段 | 频数(人数) |
第 |
|
|
第 |
|
|
第 |
|
|
第 |
|
|
第 |
|
|
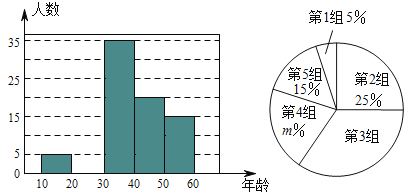
(1)请直接写出![]() ,第
,第![]() 组人数在扇形统计图中所对应的圆心角是 度;
组人数在扇形统计图中所对应的圆心角是 度;
(2)请补全上面的频数分布直方图:
(3)假设该市现有![]() 岁的市民
岁的市民![]() 万人,问
万人,问![]() 岁年龄段的关注创建文明城市的人数约有多少?
岁年龄段的关注创建文明城市的人数约有多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线与![]() 轴交于
轴交于![]() ,
,![]() 点,与
点,与![]() 轴交于点
轴交于点![]() ,抛物线的顶点为
,抛物线的顶点为![]() ,连接
,连接![]() .
.
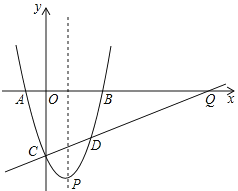
(1)求此抛物线的表达式;
(2)在抛物线上找一点![]() ,使得
,使得![]() 与
与![]() 垂直,且直线
垂直,且直线![]() 与
与![]() 轴交于点
轴交于点![]() ,求点
,求点![]() 的坐标;
的坐标;
(3)抛物线对称轴上是否存在一点![]() ,使得
,使得![]() ,若存在,求出
,若存在,求出![]() 点坐标;若不存在,请说明理由.
点坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com