
【题目】如图,![]() 是
是![]() 的直径,
的直径,![]() 为
为![]() 的弦,
的弦,![]() ,
,![]() 与
与![]() 的延长线交于点
的延长线交于点![]() ,点
,点![]() 在
在![]() 上, 满足
上, 满足![]() .
.
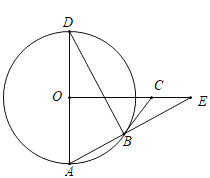
(1)求证:![]() 是
是![]() 的切线;
的切线;
(2)若![]() ,
,![]() , 求线段
, 求线段![]() 的长.
的长.
【答案】(1)见解析;(2)![]() .
.
【解析】
(1)连接OB,如图,根据圆周角定理得到∠ABD=90°,再根据等腰三角形的性质和已知条件证出∠OBC=90°,即可得出结论;
(2)根据圆周角定理得到∠ABD=90°,得到∠A=60°,求得∠E=30°,根据等腰三角形的性质得到CE=CB,根据三角形外角的性质得到∠BCO=60°,解直角三角形即可得到结论.
(1)证明:连接OB,如图,
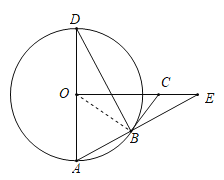
∵AD是⊙O的直径,
∴∠ABD=90°,
∴∠A+∠ADB=90°,
∵OA=OB,
∴∠A=∠OBA,
∵∠CBE=∠ADB,
∴∠OBA+∠CBE=90°,
∴∠OBC=180°-90°=90°,
∴BC⊥OB,
∴BC是⊙O的切线;
(2)∵AD是⊙O的直径,
∴∠ABD=90°,
∴∠A=60°,
∵OE⊥AD,
∴∠AOE=90°,
∴∠E=30°,
∵∠CBE=30°,
∴∠CBE=∠E=30°,
∴CE=CB,
∴∠BCO=60°,
在![]() 中
中
![]()
![]()
∴BC=![]() OB=
OB=![]() ,
,
∴CE=![]() .
.


 优百分课时互动系列答案
优百分课时互动系列答案 开心蛙状元作业系列答案
开心蛙状元作业系列答案科目:初中数学 来源: 题型:
【题目】小吴家准备购买一台电视机,小吴将收集到的某地区A、B、C三种品牌电视机销售情况的有关数据统计如下:
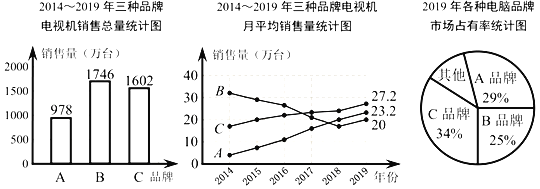
根据上述三个统计图,请解答:
(1)2014~2019年三种品牌电视机销售总量最多的是 品牌,月平均销售量最稳定的是 品牌.
(2)2019年其他品牌的电视机年销售总量是多少万台?
(3)货比三家后,你建议小吴家购买哪种品牌的电视机?说说你的理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若二次函数![]() 的图象与
的图象与![]() 轴分别交于点
轴分别交于点![]() 、
、![]() ,且过点
,且过点![]() .
.
(1)求二次函数表达式;
(2)若点![]() 为抛物线上第一象限内的点,且
为抛物线上第一象限内的点,且![]() ,求点
,求点![]() 的坐标;
的坐标;
(3)在抛物线上(![]() 下方)是否存在点
下方)是否存在点![]() ,使
,使![]() ?若存在,求出点
?若存在,求出点![]() 到
到![]() 轴的距离;若不存在,请说明理由.
轴的距离;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,济南市为加快![]() 网络建设,某通信公司在一个坡度为
网络建设,某通信公司在一个坡度为![]() 的山腰上建了一座垂直于水平面的
的山腰上建了一座垂直于水平面的![]() 信号通信塔
信号通信塔![]() ,在距山脚
,在距山脚![]() 处水平距离
处水平距离![]() 的点
的点![]() 处测得通信塔底
处测得通信塔底![]() 处的仰角是
处的仰角是![]() ,通信塔顶
,通信塔顶![]() 处的仰角是
处的仰角是![]() .则通信塔的高度
.则通信塔的高度![]() 为( )(结果保留整数,参考数据:
为( )(结果保留整数,参考数据:![]() ,
,![]() )
)

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
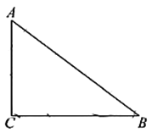
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() .点
.点![]() 从点
从点![]() 出发,以每秒5个单位长度的速度沿
出发,以每秒5个单位长度的速度沿![]() 向终点
向终点![]() 运动,同时点
运动,同时点![]() 从点
从点![]() 出发,以相同的速度沿
出发,以相同的速度沿![]() 向终点
向终点![]() 运动,过点
运动,过点![]() 作
作![]() 于点
于点![]() ,连结
,连结![]() ,以
,以![]() 、
、![]() 为邻边作矩形
为邻边作矩形![]() ,当点
,当点![]() 运动到终点时,整个运动停止,设矩形
运动到终点时,整个运动停止,设矩形![]() 与
与![]() 重叠部分图形的面积为
重叠部分图形的面积为![]() ,点
,点![]() 的运动时间为
的运动时间为![]() 秒.
秒.
(1)①![]() 的长为 ;
的长为 ;
②用含![]() 的代数式表示线段
的代数式表示线段![]() 的长为 ;
的长为 ;
(2)当![]() 的长度为10时,求
的长度为10时,求![]() 的值;
的值;
(3)求![]() 与
与![]() 的函数关系式;
的函数关系式;
(4)当过点![]() 和点
和点![]() 的直线垂直于
的直线垂直于![]() 的一边时,直接写出
的一边时,直接写出![]() 的值.
的值.
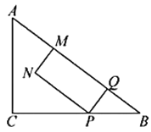
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着![]() 技术的发展,人们对各类
技术的发展,人们对各类![]() 产品的使用充满期待.某公司计划在某地区销售第一款
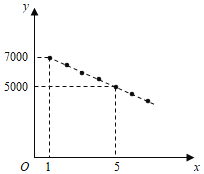
产品的使用充满期待.某公司计划在某地区销售第一款![]() 产品,根据市场分析,该产品的销售价格将随销售周期的变化而变化.设该产品在第
产品,根据市场分析,该产品的销售价格将随销售周期的变化而变化.设该产品在第![]() (
(![]() 为正整数)个销售周期每台的销售价格为
为正整数)个销售周期每台的销售价格为![]() 元,
元,![]() 与
与![]() 之间满足如图所示的一次函数关系.
之间满足如图所示的一次函数关系.
(1)求![]() 与
与![]() 之间的关系式;
之间的关系式;
(2)设该产品在第![]() 个销售周期的销售数量为
个销售周期的销售数量为![]() (万台),
(万台),![]() 与
与![]() 的关系可用
的关系可用![]() 来描述.根据以上信息,试问:哪个销售周期的销售收入最大?此时该产品每台的销售价格是多少元?
来描述.根据以上信息,试问:哪个销售周期的销售收入最大?此时该产品每台的销售价格是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
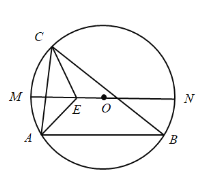
【题目】如图,![]() 是
是![]() 的直径,弦
的直径,弦![]() 点
点![]() 是直径
是直径![]() 上方半圆上的动点(包括端点
上方半圆上的动点(包括端点![]() 和
和![]() 的平分线相交于点E,当点
的平分线相交于点E,当点![]() 从点
从点![]() 运动到点
运动到点![]() 时,则
时,则![]() 两点的运动路径长的比值是( )
两点的运动路径长的比值是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com