
【题目】如图,济南市为加快![]() 网络建设,某通信公司在一个坡度为
网络建设,某通信公司在一个坡度为![]() 的山腰上建了一座垂直于水平面的
的山腰上建了一座垂直于水平面的![]() 信号通信塔
信号通信塔![]() ,在距山脚
,在距山脚![]() 处水平距离
处水平距离![]() 的点
的点![]() 处测得通信塔底
处测得通信塔底![]() 处的仰角是
处的仰角是![]() ,通信塔顶
,通信塔顶![]() 处的仰角是
处的仰角是![]() .则通信塔的高度
.则通信塔的高度![]() 为( )(结果保留整数,参考数据:
为( )(结果保留整数,参考数据:![]() ,
,![]() )
)

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
科目:初中数学 来源: 题型:
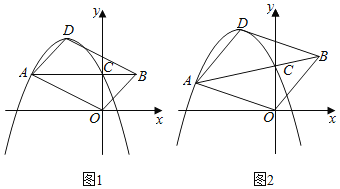
【题目】如图,已知在平面直角坐标系xOy中,抛物线y=﹣x2+bx+c(c>0)的顶点为D,与y轴的交点为C.过点C的直线CA与抛物线交于另一点A(点A在对称轴左侧),点B在AC的延长线上,连结OA,OB,DA和DB.
(1)如图1,当AC∥x轴时,
①已知点A的坐标是(﹣2,1),求抛物线的解析式;
②若四边形AOBD是平行四边形,求证:b2=4c.
(2)如图2,若b=﹣2,![]() =
=![]() ,是否存在这样的点A,使四边形AOBD是平行四边形?若存在,求出点A的坐标;若不存在,请说明理由.
,是否存在这样的点A,使四边形AOBD是平行四边形?若存在,求出点A的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“切实减轻学生课业负担”是我市作业改革的一项重要举措.某中学为了解本校学生平均每天的课外作业时间,随机抽取部分学生进行问卷调查,并将调查结果分为A、B、C、D四个等级,A:1小时以内;B:1小时--1.5小时;C:1.5小时--2小时;D:2小时以上.根据调查结果绘制了如图所示的两种不完整的统计图,请根据图中信息解答下列问题:
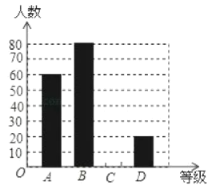
(1)该校共调查了多少名学生?
(2)请将条形统计图补充完整;
(3)在此次调查问卷中,甲、乙两班各有2人平均每天课外作业量都是2小时以上,从这4人中人选2人去参加座谈,用列表或画树状图的方法求选出的2人来自不同班级的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
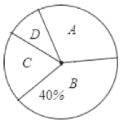
【题目】某校组织学生书法比赛,对参赛作品按A、B、C、D四个等级进行了评定.现随机取部分学生书法作品的评定结果进行分析,并绘制扇形统计图和条形统计图如下:

根据上述信息完成下列问题:
(1)求这次抽取的样本的容量;
(2)请在图②中把条形统计图补充完整;
(3)已知该校这次活动共收到参赛作品750份,请你估计参赛作品达到B级以上(即A级和B级)有多少份?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我市实施城乡生活垃圾分类管理,推进生态文明建设为增强学生的环保意识,随机抽取![]() 名学生,对他们的垃圾分类投放情况进行调查,这
名学生,对他们的垃圾分类投放情况进行调查,这![]() 名学生分别标记为
名学生分别标记为![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,其中“√”表示投放正确,“×”表示投放错误,统计情况如下表.
,其中“√”表示投放正确,“×”表示投放错误,统计情况如下表.
学生 垃圾类别 |
|
|
|
|
|
|
|
|
厨余垃圾 | √ | √ | √ | √ | √ | √ | √ | √ |
可回收垃圾 | √ | × | √ | × | × | √ | √ | √ |
有害垃圾 | × | √ | × | √ | √ | × | × | √ |
其他垃圾 | × | √ | √ | × | × | √ | √ | √ |
(1)求![]() 名学生中至少有三类垃圾投放正确的概率;
名学生中至少有三类垃圾投放正确的概率;
(2)为进一步了解垃圾分类投放情况,现从![]() 名学生里“有害垃圾”投放错误的学生中随机抽取两人接受采访,试用标记的字母列举所有可能抽取的结果,并求出刚好抽到
名学生里“有害垃圾”投放错误的学生中随机抽取两人接受采访,试用标记的字母列举所有可能抽取的结果,并求出刚好抽到![]() 、
、![]() 两位学生的概率.
两位学生的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了了解某校九年级学生体育测试成绩情况,现从中随机抽取部分学生的体育成绩,并用得到的数据绘制了统计图①和图②,请根据图中提供的信息,回答下列问题:
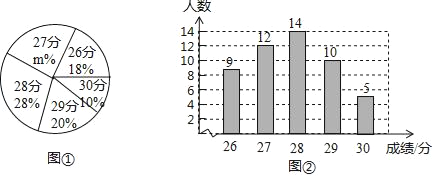
(1)本次随机抽样调查的学生人数为______,图①中的m的值为______;
(2)求本次抽样调查获取的样本数据的众数、中位数和平均数;
(3)若该校九年级共有学生300人,如果体育成绩达28分以上(含28分)为优秀,请估计该校九年级学生体育成绩达到优秀的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学数学兴趣小组在一次课外学习与探究中遇到一些新的数学符号,他们将其中某些材料摘录如下:
对于三个实数a,b,c,用M{a,b,c}表示这三个数的平均数,用min{a,b,c}表示这三个数中最小的数.例如:M{1,2,9}=![]() =4,min{1,2,﹣3}=﹣3,min{3,1,1}=1.请结合上述材料,解决下列问题:
=4,min{1,2,﹣3}=﹣3,min{3,1,1}=1.请结合上述材料,解决下列问题:
(1)①M{(﹣2)2,22,﹣22}= ; ②min{sin30°,cos60°,tan45°}= ;
(2)若M{﹣2x,x2,3}=2,求x的值;
(3)若min{3﹣2x,1+3x,﹣5}=﹣5,求x的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com