
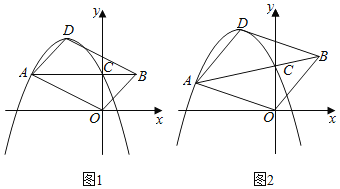
【题目】如图,已知在平面直角坐标系xOy中,抛物线y=﹣x2+bx+c(c>0)的顶点为D,与y轴的交点为C.过点C的直线CA与抛物线交于另一点A(点A在对称轴左侧),点B在AC的延长线上,连结OA,OB,DA和DB.
(1)如图1,当AC∥x轴时,
①已知点A的坐标是(﹣2,1),求抛物线的解析式;
②若四边形AOBD是平行四边形,求证:b2=4c.
(2)如图2,若b=﹣2,![]() =
=![]() ,是否存在这样的点A,使四边形AOBD是平行四边形?若存在,求出点A的坐标;若不存在,请说明理由.
,是否存在这样的点A,使四边形AOBD是平行四边形?若存在,求出点A的坐标;若不存在,请说明理由.
【答案】(1)①y=﹣x2﹣2x+1;②证明见解析;(2)存在这样的点A,A(﹣![]() ,
,![]() )
)
【解析】
(1)①由点A(﹣2,1)得到C(0,1),利用待定系数法即可求解;
②作DE⊥x轴于E,交AB于点F,利用顶点坐标及点C的坐标求得DF=![]() ,利用“AAS”证得△AFD≌△BCO,得到DF=OC,即可证得结论;
,利用“AAS”证得△AFD≌△BCO,得到DF=OC,即可证得结论;
(2)由题意知顶点坐标D(﹣1,c+1),设点A(m,﹣m2﹣2m+c),利用“AAS”证得△AFD≌△BCO,作如图的辅助线,证得△ANF∽△AMC,结合已知![]() =
=![]() ,求得
,求得![]() ,利用比例线段即可求解.
,利用比例线段即可求解.
(1)①∵AC∥x轴,点A(﹣2,1),
∴C(0,1),
将点A(﹣2,1),C(0,1)代入抛物线解析式中,得:
![]() ,
,
∴![]() ,
,
∴抛物线的解析式为y=﹣x2﹣2x+1;
②如图1,过点D作DE⊥x轴于E,交AB于点F,
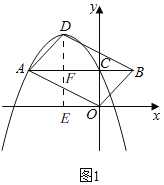
∵AC∥x轴,
∴EF=OC=c,
∵点D是抛物线的顶点坐标,
∴D(![]() ,
,![]() ),
),
∴DF=DE﹣EF=![]() =
=![]() ,
,
∵四边形AOBD是平行四边形,
∴AD=OB,AD∥OB,
∴∠DAF=∠OBC,
∵∠AFD=∠BCO=90°,
∴△AFD≌△BCO(AAS),
∴DF=OC,
∴![]() =c,
=c,
即b2=4c;
(2)如图2,
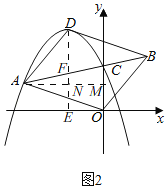
∵b=﹣2.
∴抛物线的解析式为y=﹣x2﹣2x+c,
∴顶点坐标D(﹣1,c+1),
假设存在这样的点A使四边形AOBD是平行四边形,
设点A(m,﹣m2﹣2m+c)(m<0),
过点D作DE⊥x轴于点E,交AB于F,
∴∠AFD=∠EFC=∠BCO,
∵四边形AOBD是平行四边形,
∴AD=BO,AD∥OB,
∴∠DAF=∠OBC,
∴△AFD≌△BCO(AAS),
∴AF=BC,DF=OC,
过点A作AM⊥y轴于M,交DE于N,
∴DE∥CO,
∴△ANF∽△AMC,
∴![]() =
=![]() ,
,
∵AM=﹣m,AN=AM﹣NM=﹣m﹣1,
∴![]() ,
,
∴![]() ,
,
∴点A的纵坐标为﹣(﹣![]() )2﹣2×(﹣
)2﹣2×(﹣![]() )+c=c﹣
)+c=c﹣![]() <c,
<c,
∵AM∥x轴,
∴点M的坐标为(0,c﹣![]() ),N(﹣1,c﹣
),N(﹣1,c﹣![]() ),
),
∴CM=c﹣(c﹣![]() )=
)=![]() ,
,
∵点D的坐标为(﹣1,c+1),
∴DN=(c+1)﹣(c﹣![]() )=
)=![]() ,
,
∵DF=OC=c,
∴FN=DN﹣DF=![]() ﹣c,
﹣c,
∵![]() =
=![]() ,
,
∴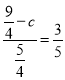 ,
,
∴c=![]() ,
,
∴c﹣![]() =
=![]() ,
,
∴点A纵坐标为![]() ,
,
∴A(﹣![]() ,
,![]() ),
),
∴存在这样的点A,使四边形AOBD是平行四边形.


科目:初中数学 来源: 题型:
【题目】某商场第一次用11000元购进某款拼装机器人进行销售,很快销售一空,商家又用24000元第二次购进同款机器人,所购进数量是第一次的2倍,但单价贵了10元.
(1)求该商家第一次购进机器人多少个?
(2)若在这两次机器人的销售中,该商场全部售完,而且售价都是130元,问该商场总共获利多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为倡导健康环保,自带水杯已成为一种好习惯,某超市销售甲,乙两种型号水杯,进价和售价均保持不变,其中甲种型号水杯进价为25元/个,乙种型号水杯进价为45元/个,下表是前两月两种型号水杯的销售情况:
时间 | 销售数量(个) | 销售收入(元)(销售收入=售价×销售数量) | |
甲种型号 | 乙种型号 | ||
第一月 | 22 | 8 | 1100 |
第二月 | 38 | 24 | 2460 |
(1)求甲、乙两种型号水杯的售价;
(2)第三月超市计划再购进甲、乙两种型号水杯共80个,这批水杯进货的预算成本不超过2600元,且甲种型号水杯最多购进55个,在80个水杯全部售完的情况下设购进甲种号水杯a个,利润为w元,写出w与a的函数关系式,并求出第三月的最大利润.
查看答案和解析>>
科目:初中数学 来源: 题型:
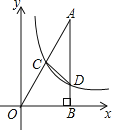
【题目】如图,已知在平面直角坐标系xOy中,Rt△OAB的直角顶点B在x轴的正半轴上,点A在第一象限,反比例函数y=![]() (x>0)的图象经过OA的中点C.交AB于点D,连结CD.若△ACD的面积是2,则k的值是_____.
(x>0)的图象经过OA的中点C.交AB于点D,连结CD.若△ACD的面积是2,则k的值是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小吴家准备购买一台电视机,小吴将收集到的某地区A、B、C三种品牌电视机销售情况的有关数据统计如下:
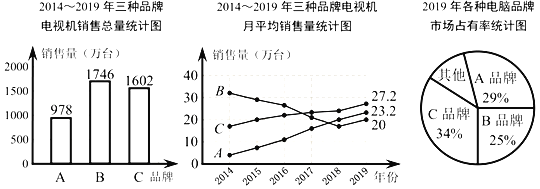
根据上述三个统计图,请解答:
(1)2014~2019年三种品牌电视机销售总量最多的是 品牌,月平均销售量最稳定的是 品牌.
(2)2019年其他品牌的电视机年销售总量是多少万台?
(3)货比三家后,你建议小吴家购买哪种品牌的电视机?说说你的理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
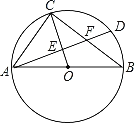
【题目】如图,△ABC内接于⊙O,AB为⊙O的直径,AB=10,AC=6,连结OC,弦AD分别交OC,BC于点E,F,其中点E是AD的中点.
(1)求证:∠CAD=∠CBA.
(2)求OE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
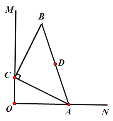
【题目】如图,∠MON =∠ACB = 90°,AC = BC,AB =5,△ABC顶点A、C分别在ON、OM上,点D是AB边上的中点,当点A在边ON上运动时,点C随之在边OM上运动,则OD的最大值为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,济南市为加快![]() 网络建设,某通信公司在一个坡度为
网络建设,某通信公司在一个坡度为![]() 的山腰上建了一座垂直于水平面的
的山腰上建了一座垂直于水平面的![]() 信号通信塔
信号通信塔![]() ,在距山脚
,在距山脚![]() 处水平距离
处水平距离![]() 的点
的点![]() 处测得通信塔底
处测得通信塔底![]() 处的仰角是
处的仰角是![]() ,通信塔顶
,通信塔顶![]() 处的仰角是
处的仰角是![]() .则通信塔的高度
.则通信塔的高度![]() 为( )(结果保留整数,参考数据:
为( )(结果保留整数,参考数据:![]() ,
,![]() )
)

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com