
����Ŀ��С���������һ̨���ӻ���С�⽫�ռ�����ij����A��B��C����Ʒ�Ƶ��ӻ�����������й�����ͳ�����£�
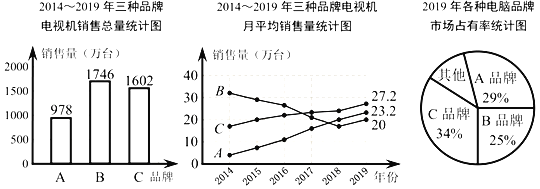
������������ͳ��ͼ������
��1��2014��2019������Ʒ�Ƶ��ӻ����������������� ��Ʒ�ƣ���ƽ�����������ȶ������� ��Ʒ�ƣ�
��2��2019������Ʒ�Ƶĵ��ӻ������������Ƕ�����̨��
��3���������Һ��㽨��С��ҹ�������Ʒ�Ƶĵ��ӻ���˵˵������ɣ�
���𰸡���1��B�� C����2��2019������Ʒ�Ƶĵ��ӻ�������������115.2��̨����3�����鹺��CƷ�ƣ����鹺��BƷ�ƣ������ɼ�����
��������
��1��������ͳ��ͼ������ͳ��ͼ���Եó��𰸣�
��2���������������������������ռ�İٷֱȣ�
��3�����г�ռ���ʡ�ƽ���������ȷ���������飮
�⣺��1��������ͳ��ͼ�ɵã�2014��2019������Ʒ�Ƶ��ӻ���������������BƷ�ƣ���1746��̨��
������ͳ��ͼ�ɵã�2014��2019������Ʒ�Ƶ��ӻ���ƽ�����������ȶ�����CƷ�ƣ��Ƚ��ȶ���������С��
�ʴ�Ϊ��B��C��
��2����20��12��25%��960����̨����1��25%��29%��34%��12%��
��960��12%��115.2����̨����
��2019������Ʒ�Ƶĵ��ӻ�������������115.2��̨��
��3�����鹺��CƷ�ƣ���ΪCƷ��2019����г�ռ������ߣ���5��������������ȶ���
���鹺��BƷ�ƣ���ΪBƷ�Ƶ�����������࣬�ܵ����˿͵�������



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
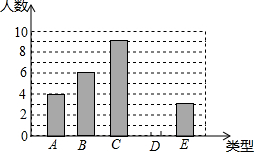
����Ŀ��ij��λ750��ְ�������μ���ƶ������ѧУ������Ϊ�˽�ְ���ľ�������������������ķ�����ȡ30��ְ����Ϊ�����������ǵľ���������ͳ�ƣ�ͳ�ƽ������4����5����6����7����8�����࣬�ֱ���A��B��C��D��E��ʾ������ͳ�����ݻ��Ƴ�����ͼ��ʾ�IJ�����������ͳ��ͼ����ͼ�и�������Ϣ����������⣺
��1����ȫ����ͳ��ͼ��
��2������30��ְ�����鱾����ƽ��������������λ����
��3�����Ƹõ�λ750��ְ����������ٱ���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
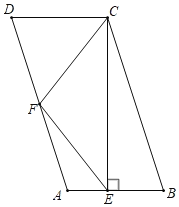
����Ŀ����ͼ�����ı���ABCD�У�AD��BC��AD=BC=2AB��F��AD���е㣬��CE��AB������E���߶�AB�ϣ�����EF��CF��
��1������ADC=80�㣬���ECF��
��2����֤����ECF=��CEF��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪OT��Rt��ABOб��AB�ϵĸ��ߣ�AO=BO����OΪԲ�ģ�OTΪ�뾶��Բ��OA�ڵ�C������C����O������CD����AB�ڵ�D�������н����д�����ǣ�������
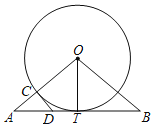
A.DC=DTB.AD=![]() DTC.BD=BOD.2OC=5AC
DTC.BD=BOD.2OC=5AC
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
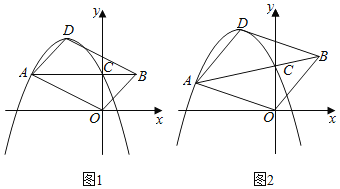
����Ŀ����ͼ����֪��ƽ��ֱ������ϵxOy�У�������y����x2+bx+c(c��0)�Ķ���ΪD����y��Ľ���ΪC������C��ֱ��CA�������߽�����һ��A(��A�ڶԳ������)����B��AC���ӳ����ϣ�����OA��OB��DA��DB��
(1)��ͼ1����AC��x��ʱ��
����֪��A��������(��2��1)���������ߵĽ���ʽ��
�����ı���AOBD��ƽ���ı��Σ���֤��b2��4c��
(2)��ͼ2����b����2��![]() ��
��![]() ���Ƿ���������ĵ�A��ʹ�ı���AOBD��ƽ���ı��Σ������ڣ������A�����ꣻ�������ڣ���˵�����ɣ�
���Ƿ���������ĵ�A��ʹ�ı���AOBD��ƽ���ı��Σ������ڣ������A�����ꣻ�������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
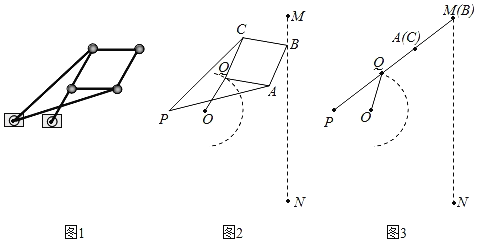
����Ŀ��ͼ1�����߸��������Ӷ��ɵĻ�еװ�ã�ͼ2����ʾ��ͼ����֪O��P����̶�������PA=PC=140cm��AB=BC=CQ=QA=60cm��OQ=50cm��O��P��������OQ������ȣ���OQ�Ƶ�Oת��ʱ����A��B��C��λ����֮�ı䣬��Bǡ�����߶�MN�������˶�������B�˶�����M��Nʱ����A��C�غϣ���P��Q��A��B��ͬһֱ���ϣ���ͼ3����
��1����P��MN�ľ���Ϊ_____cm��
��2������P��O��A��ͬһֱ����ʱ����Q��MN�ľ���Ϊ_____cm��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����һ�����ǰ��һ�ŶԱ�ƽ�е�ֽ������ͼ�ķ�ʽ�ڷţ���A����DEF��90������EDF��45������ABC��30������E��F���ڱ�AB�ϣ���D��ֽ����һ���ϣ�����BC��ֽ������һ���غϣ�������Ķ����ǣ�������
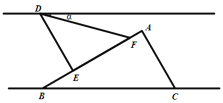
A.15��B.22��5��C.30��D.45��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
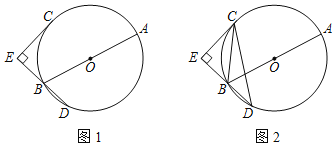
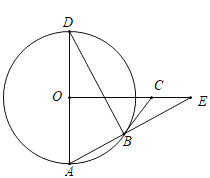
����Ŀ����֪��ABΪ��O��ֱ����C��DΪ����O�ϵĵ㣬C���Ż�AD���е㣬CE��DB��DB���ӳ����ڵ�E��
��1����ͼ1���ж�ֱ��CE����O��λ�ù�ϵ����˵�����ɣ�
��2����ͼ2����tan��BCE��![]() ����BC��CD����cos��BCD��ֵ��
����BC��CD����cos��BCD��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��![]() ��
��![]() ��ֱ����
��ֱ����![]() Ϊ
Ϊ![]() ���ң�
���ң�![]() ��
��![]() ��
��![]() ���ӳ��߽��ڵ�
���ӳ��߽��ڵ�![]() ����
����![]() ��
��![]() �ϣ� ����
�ϣ� ����![]() ��
��
��1����֤��![]() ��
��![]() �����ߣ�
�����ߣ�
��2����![]() ��
��![]() �� ���߶�
�� ���߶�![]() �ij���
�ij���
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com