
【题目】如图,已知OT是Rt△ABO斜边AB上的高线,AO=BO.以O为圆心,OT为半径的圆交OA于点C,过点C作⊙O的切线CD,交AB于点D.则下列结论中错误的是( )
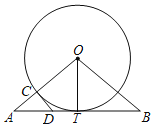
A.DC=DTB.AD=![]() DTC.BD=BOD.2OC=5AC
DTC.BD=BOD.2OC=5AC
【答案】D
【解析】
根据切线的判定知DT是⊙O的切线,根据切线长定理可判断选项A正确;可证得△ADC是等腰直角三角形,可计算判断选项B正确;根据切线的性质得到CD=CT,根据全等三角形的性质得到∠DOC=∠TOC,根据三角形的外角的性质可判断选项C正确;
解:如图,连接OD.
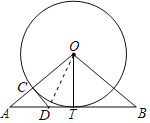
∵OT是半径,OT⊥AB,
∴DT是⊙O的切线,
∵DC是⊙O的切线,
∴DC=DT,故选项A正确;
∵OA=OB,∠AOB=90°,
∴∠A=∠B=45°,
∵DC是切线,
∴CD⊥OC,
∴∠ACD=90°,
∴∠A=∠ADC=45°,
∴AC=CD=DT,
∴AD=![]() CD=
CD=![]() DT,故选项B正确;
DT,故选项B正确;
∵OD=OD,OC=OT,DC=DT,
∴△DOC≌△DOT(SSS),
∴∠DOC=∠DOT,
∵OA=OB,OT⊥AB,∠AOB=90°,
∴∠AOT=∠BOT=45°,
∴∠DOT=∠DOC=22.5°,
∴∠BOD=∠ODB=67.5°,
∴BO=BD,故选项C正确;
∵OA=OB,∠AOB=90°,OT⊥AB,
设⊙O的半径为2,
∴OT=OC=AT=BT=2,
∴OA=OB=2![]() ,
,
∴![]() ,
,
2OC![]() 5AC故选项D错误;
5AC故选项D错误;
故选:D.


科目:初中数学 来源: 题型:
【题目】如图所示,△ABC内接于⊙O,且AB为⊙O的直径,作![]() 的平分线交圆周于点D,连结AD、BD,AB、CD交于点E.
的平分线交圆周于点D,连结AD、BD,AB、CD交于点E.

(1)求证:△ABD为等腰直角三角形;
(2)填空:
①若![]() ,则AE的长度为_______;
,则AE的长度为_______;
②在①的条件下,延长AC、DB交于点P,则![]() ______.
______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是一垂直于水平面的建筑物,某同学从建筑物底端B出发,先沿水平方向向右行走20米到达点C,再经过一段坡度(或坡比)为i=1:0.75、坡长为10米的斜坡CD到达点D,然后再沿水平方向向右行走40米到达点E(A,B,C,D,E均在同一平面内),在E处处测得建筑物顶端A的仰角为24°,则建筑物AB的高度约为__米.(参考数据:sin24°≈0.41,cos24°≈0.91,tan24°≈0.45)
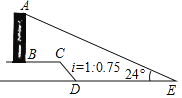
查看答案和解析>>
科目:初中数学 来源: 题型:
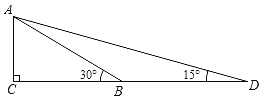
【题目】构建几何图形解决代数问题是“数形结合”思想的重要性,在计算tan15°时,如图.在Rt△ACB中,∠C=90°,∠ABC=30°,延长CB使BD=AB,连接AD,得∠D=15°,所以tan15°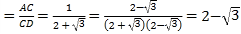 .类比这种方法,计算tan22.5°的值为( )
.类比这种方法,计算tan22.5°的值为( )
A.![]() B.
B.![]() ﹣1C.
﹣1C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为倡导健康环保,自带水杯已成为一种好习惯,某超市销售甲,乙两种型号水杯,进价和售价均保持不变,其中甲种型号水杯进价为25元/个,乙种型号水杯进价为45元/个,下表是前两月两种型号水杯的销售情况:
时间 | 销售数量(个) | 销售收入(元)(销售收入=售价×销售数量) | |
甲种型号 | 乙种型号 | ||
第一月 | 22 | 8 | 1100 |
第二月 | 38 | 24 | 2460 |
(1)求甲、乙两种型号水杯的售价;
(2)第三月超市计划再购进甲、乙两种型号水杯共80个,这批水杯进货的预算成本不超过2600元,且甲种型号水杯最多购进55个,在80个水杯全部售完的情况下设购进甲种号水杯a个,利润为w元,写出w与a的函数关系式,并求出第三月的最大利润.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某企业承接了27000件产品的生产任务,计划安排甲、乙两个车间的共50名工人,合作生产20天完成.已知甲、乙两个车间利用现有设备,工人的工作效率为:甲车间每人每天生产25件,乙车间每人每天生产30件.
(1)求甲、乙两个车间各有多少名工人参与生产?
(2)为了提前完成生产任务,该企业设计了两种方案:
方案一 甲车间租用先进生产设备,工人的工作效率可提高20%,乙车间维持不变.
方案二 乙车间再临时招聘若干名工人(工作效率与原工人相同),甲车间维持不变.
设计的这两种方案,企业完成生产任务的时间相同.
①求乙车间需临时招聘的工人数;
②若甲车间租用设备的租金每天900元,租用期间另需一次性支付运输等费用1500元;乙车间需支付临时招聘的工人每人每天200元.问:从新增加的费用考虑,应选择哪种方案能更节省开支?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小吴家准备购买一台电视机,小吴将收集到的某地区A、B、C三种品牌电视机销售情况的有关数据统计如下:
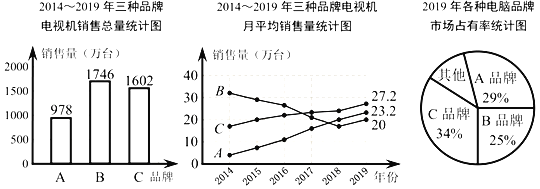
根据上述三个统计图,请解答:
(1)2014~2019年三种品牌电视机销售总量最多的是 品牌,月平均销售量最稳定的是 品牌.
(2)2019年其他品牌的电视机年销售总量是多少万台?
(3)货比三家后,你建议小吴家购买哪种品牌的电视机?说说你的理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
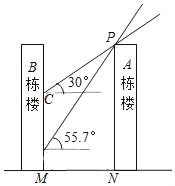
【题目】如图,某小区A栋楼在B栋楼的南侧,两楼高度均为90m,楼间距为MN.春分日正午,太阳光线与水平面所成的角为55.7°,A栋楼在B栋楼墙面上的影高为DM;冬至日正午,太阳光线与水平面所成的角为30°,A栋楼在B栋楼墙面上的影高为CM.已知CD=44.5m.
(1)求楼间距MN;
(2)若B号楼共30层,每层高均为3m,则点C位于第几层?(参考数据:tan30°≈0.58,sin55.7°≈0.83,cos55.7°≈0.56,tan55.7°≈1.47)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com