
【题目】如图所示,△ABC内接于⊙O,且AB为⊙O的直径,作![]() 的平分线交圆周于点D,连结AD、BD,AB、CD交于点E.
的平分线交圆周于点D,连结AD、BD,AB、CD交于点E.

(1)求证:△ABD为等腰直角三角形;
(2)填空:
①若![]() ,则AE的长度为_______;
,则AE的长度为_______;
②在①的条件下,延长AC、DB交于点P,则![]() ______.
______.
【答案】(1)见解析;(2)①![]() ;②6.
;②6.
【解析】
(1)由AB为直径,则![]() ,由角平分线和圆周角定理,得到
,由角平分线和圆周角定理,得到![]() ,即可得到结论;
,即可得到结论;
(2)①作![]() ,则
,则![]() ,由三角形的面积之比,得到
,由三角形的面积之比,得到![]() ,然后求出AB的长度,即可得到答案;
,然后求出AB的长度,即可得到答案;
②由题意,先证明△ADP∽△BCP,则![]() ,根据比例进行计算,即可得到答案.
,根据比例进行计算,即可得到答案.
(1)证明:∵CD平分![]()
∴![]()
∵![]()
∴![]()
∴![]()
∵AB为⊙O的直径
∴![]()
∴△ABD为等腰直角三角形;
(2)作![]() ,如图1所示:
,如图1所示:
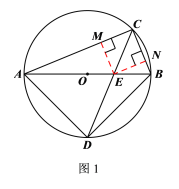
∵CD平分![]() ,
,![]() ,
,
∴![]()
∵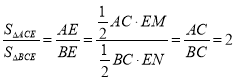 ,
,
∴![]() ,
,
∴![]() ,
,
在Rt△ABC(AB为⊙O的直径)中,由勾股定理得:
![]()
∴![]() ;
;
故答案为:![]() ;
;
②如图:

由①可知,![]() ,△ABD为等腰直角三角形,
,△ABD为等腰直角三角形,
∴![]() ,
,
∵∠ADB=∠BCP=90°,∠P=∠P,
∴△ADP∽△BCP,
∴![]() ,
,
∵![]() ,
,![]() ,
,
∴![]() ,
,
解得:![]() ,
,![]() ,
,
故答案为:6;


科目:初中数学 来源: 题型:
【题目】磐是我国国带的一种打击乐器和礼器(如图),据先秦文献《吕氏春秋古乐篇》记载:尧命击磐“以象上帝”“以致舞百兽”,描绘出一幅古老的原始社会的乐舞生活场景.20世纪70年代在山西夏县出土了一件大石磐,上部有一穿孔,击之声音悦耳,经测定,此磐据经约4000年,属于夏代的遗存,这是迄今发现最早的磐的实物.从正面看磐是一个多边形图案(如图2),已知MN为地面,测得AB=30厘米,BC=20厘米,∠BCN=60°,∠ABC=95°,求磐的最高点A到地面MN的高度h.(参考数据:sin55°≈0.82,cos55°≈0.57,tan55°≈1.43,![]() ≈1.73,结果保留一位小数)
≈1.73,结果保留一位小数)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在菱形ABCD中,AB=2,∠ABC=60°,对角线AC、BD相交于点O,将对角线AC所在的直线绕点O顺时针旋转角α(0°<α<90°)后得直线l,直线l与AD、BC两边分别相交于点E和点F.
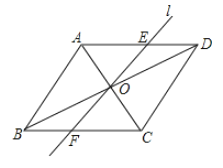
(1)求证:△AOE≌△COF;
(2)当α=30°时,求线段EF的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一方有难,八方支援.“新冠肺炎”疫情来袭,除了医务人员主动请缨逆行走向战场外,众多企业也伸出援助之手.某公司用甲,乙两种货车向武汉运送爱心物资,两次满载的运输情况如下表:
甲种货车辆数 | 乙种货车辆数 | 合计运物资吨数 | |
第一次 | 3 | 4 | 29 |
第二次 | 2 | 6 | 31 |
(1)求甲、乙两种货车每次满载分别能运输多少吨物资;
(2)目前有46.4吨物资要运输到武汉,该公司拟安排甲乙货车共10辆,全部物资一次运完,其中每辆甲车一次运送花费500元,每辆乙车一次运送花费300元,请问该公司应如何安排车辆最节省费用?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校计划在总费用2300元的限额内,租用客车送234名学生和6名教师集体外出活动,每辆客车上至少要有1名教师.现有甲、乙两种大客车,它们的载客量和租金如下表所示.
甲种客车 | 乙种客车 | |
载客量/(人/辆) | 45 | 30 |
租金/(元/辆) | 400 | 280 |
(1)共需租多少辆客车?
(2)请给出最节省费用的租车方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,抛物线![]() 交
交![]() 轴于A、B两点,交
轴于A、B两点,交![]() 轴于点C,直线
轴于点C,直线![]() 经过点A、C.
经过点A、C.
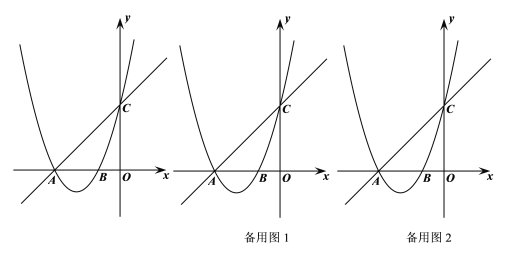
(1)求抛物线的解析式;
(2)点P为直线AC上一点,在平面内是否存在点Q,使得以A、B、P、Q为顶点的四边形为正方形?若存在,求出点Q的坐标,若不存在,请说明理由;
(3)在![]() 轴上存在点M,且
轴上存在点M,且![]() ,请直接写出点M的坐标.
,请直接写出点M的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
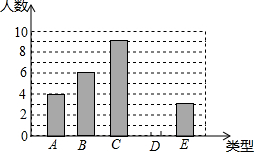
【题目】某单位750名职工积极参加向贫困地区学校捐书活动,为了解职工的捐数量,采用随机抽样的方法抽取30名职工作为样本,对他们的捐书量进行统计,统计结果共有4本、5本、6本、7本、8本五类,分别用A、B、C、D、E表示,根据统计数据绘制成了如图所示的不完整的条形统计图,由图中给出的信息解答下列问题:
(1)补全条形统计图;
(2)求这30名职工捐书本数的平均数、众数和中位数;
(3)估计该单位750名职工共捐书多少本?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“校园安全”越来越受到人们的关注,我市某中学对部分学生就校园安全知识的了解程度,采用随机抽样调查的方式,并根据收集到的信息进行统计,绘制了下面两幅尚不完整的统计图.根据图中信息回答下列问题:

(1)接受问卷调查的学生共有______人,条形统计图中m的值为______;
(2)扇形统计图中“了解很少”部分所对应扇形的圆心角的度数为______;
(3)若该中学共有学生1800人,根据上述调查结果,可以估计出该学校学生中对校园安全知识达到“非常了解”和“基本了解”程度的总人数为______人;
(4)若从对校园安全知识达到“非常了解”程度的2名男生和2名女生中随机抽取2人参加校园安全知识竞赛,请用列表或画树状图的方法,求恰好抽到1名男生和1名女生的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知OT是Rt△ABO斜边AB上的高线,AO=BO.以O为圆心,OT为半径的圆交OA于点C,过点C作⊙O的切线CD,交AB于点D.则下列结论中错误的是( )
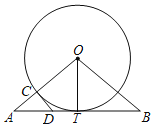
A.DC=DTB.AD=![]() DTC.BD=BOD.2OC=5AC
DTC.BD=BOD.2OC=5AC
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com