
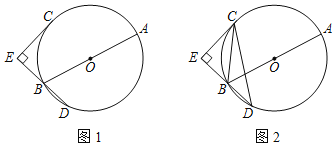
【题目】已知:AB为⊙O的直径,C、D为心⊙O上的点,C是优弧AD的中点,CE⊥DB交DB的延长线于点E.
(1)如图1,判断直线CE与⊙O的位置关系,并说明理由.
(2)如图2,若tan∠BCE=![]() ,连BC、CD,求cos∠BCD的值.
,连BC、CD,求cos∠BCD的值.
【答案】(1)直线CE与⊙O相切,理由详见解析;(2)cos∠BCD=![]() .
.
【解析】
(1)如图,作辅助线;运用圆周角定理及其推论证明∠OCE=90°,即可解决问题.
(2)首先运用切割线定理求出ED的长度;证明四边形CEDF为矩形,得到CF=DE;证明OF为△ABD的中位线;求出AF、OF的长度;进而求出OA的长度,即可解决问题.
解:(1)直线CE与⊙O相切,理由如下:
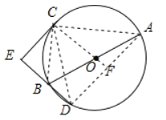
如图,连接AC,CD,BC、AD、CO,延长CO交AD于点F;
则∠CBE=∠CAD;而C是优弧ACD的中点,
∴![]() ,
,
∴∠CBA=∠CDA=∠CAD,
而∠CBE=∠CAD,∠CBA=∠OCB,
∴∠CBE=∠OCB;而CE⊥BE,
∴∠ECB+∠CBE=∠ECB+∠OCB=90°,即![]() ,
,
∴OC⊥CE,
即CE为⊙O的切线;
(2)∵tan∠BCE=![]() ,
,
设BE=4k,CE=5k,
∵CE为⊙O的切线,
∴CE2=EBED,
∴ED=![]() k,BD=
k,BD=![]() k;
k;
∵AB为⊙O的直径,
∴∠ADB=90°,而∠E=∠OCE=90°,
∴四边形CEDF为矩形,
∴OF⊥AD,AF=DF=CE=5k,
∴OF为△ABD的中位线,
∴OF=![]() BD=
BD=![]() k;由勾股定理得:OA=
k;由勾股定理得:OA=![]() =
=![]() k,
k,
∴cos∠BAD=![]() =
=![]() =
=![]() ,
,
而∠BCD=∠BAD,
∴cos∠BCD=![]() .
.


科目:初中数学 来源: 题型:
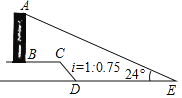
【题目】如图,AB是一垂直于水平面的建筑物,某同学从建筑物底端B出发,先沿水平方向向右行走20米到达点C,再经过一段坡度(或坡比)为i=1:0.75、坡长为10米的斜坡CD到达点D,然后再沿水平方向向右行走40米到达点E(A,B,C,D,E均在同一平面内),在E处处测得建筑物顶端A的仰角为24°,则建筑物AB的高度约为__米.(参考数据:sin24°≈0.41,cos24°≈0.91,tan24°≈0.45)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小吴家准备购买一台电视机,小吴将收集到的某地区A、B、C三种品牌电视机销售情况的有关数据统计如下:
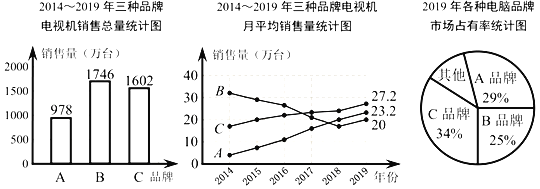
根据上述三个统计图,请解答:
(1)2014~2019年三种品牌电视机销售总量最多的是 品牌,月平均销售量最稳定的是 品牌.
(2)2019年其他品牌的电视机年销售总量是多少万台?
(3)货比三家后,你建议小吴家购买哪种品牌的电视机?说说你的理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
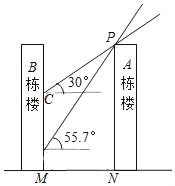
【题目】如图,某小区A栋楼在B栋楼的南侧,两楼高度均为90m,楼间距为MN.春分日正午,太阳光线与水平面所成的角为55.7°,A栋楼在B栋楼墙面上的影高为DM;冬至日正午,太阳光线与水平面所成的角为30°,A栋楼在B栋楼墙面上的影高为CM.已知CD=44.5m.
(1)求楼间距MN;
(2)若B号楼共30层,每层高均为3m,则点C位于第几层?(参考数据:tan30°≈0.58,sin55.7°≈0.83,cos55.7°≈0.56,tan55.7°≈1.47)
查看答案和解析>>
科目:初中数学 来源: 题型:
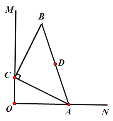
【题目】如图,∠MON =∠ACB = 90°,AC = BC,AB =5,△ABC顶点A、C分别在ON、OM上,点D是AB边上的中点,当点A在边ON上运动时,点C随之在边OM上运动,则OD的最大值为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
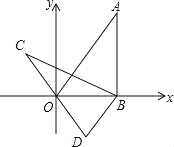
【题目】如图,在平面直角坐标系xOy中,直线y=![]() x经过点A,作AB⊥x轴于点B,将△ABO绕点B逆时针旋转60°得到△CBD,若点B的坐标为(2,0),则点C的坐标为 .
x经过点A,作AB⊥x轴于点B,将△ABO绕点B逆时针旋转60°得到△CBD,若点B的坐标为(2,0),则点C的坐标为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若二次函数![]() 的图象与
的图象与![]() 轴分别交于点
轴分别交于点![]() 、
、![]() ,且过点
,且过点![]() .
.
(1)求二次函数表达式;
(2)若点![]() 为抛物线上第一象限内的点,且
为抛物线上第一象限内的点,且![]() ,求点
,求点![]() 的坐标;
的坐标;
(3)在抛物线上(![]() 下方)是否存在点
下方)是否存在点![]() ,使
,使![]() ?若存在,求出点
?若存在,求出点![]() 到
到![]() 轴的距离;若不存在,请说明理由.
轴的距离;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着![]() 技术的发展,人们对各类
技术的发展,人们对各类![]() 产品的使用充满期待.某公司计划在某地区销售第一款
产品的使用充满期待.某公司计划在某地区销售第一款![]() 产品,根据市场分析,该产品的销售价格将随销售周期的变化而变化.设该产品在第
产品,根据市场分析,该产品的销售价格将随销售周期的变化而变化.设该产品在第![]() (
(![]() 为正整数)个销售周期每台的销售价格为
为正整数)个销售周期每台的销售价格为![]() 元,
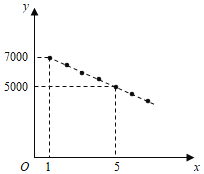
元,![]() 与
与![]() 之间满足如图所示的一次函数关系.
之间满足如图所示的一次函数关系.
(1)求![]() 与
与![]() 之间的关系式;
之间的关系式;
(2)设该产品在第![]() 个销售周期的销售数量为
个销售周期的销售数量为![]() (万台),
(万台),![]() 与
与![]() 的关系可用
的关系可用![]() 来描述.根据以上信息,试问:哪个销售周期的销售收入最大?此时该产品每台的销售价格是多少元?
来描述.根据以上信息,试问:哪个销售周期的销售收入最大?此时该产品每台的销售价格是多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com