
【题目】若二次函数![]() 的图象与
的图象与![]() 轴分别交于点
轴分别交于点![]() 、
、![]() ,且过点
,且过点![]() .
.
(1)求二次函数表达式;
(2)若点![]() 为抛物线上第一象限内的点,且
为抛物线上第一象限内的点,且![]() ,求点
,求点![]() 的坐标;
的坐标;
(3)在抛物线上(![]() 下方)是否存在点
下方)是否存在点![]() ,使
,使![]() ?若存在,求出点
?若存在,求出点![]() 到
到![]() 轴的距离;若不存在,请说明理由.
轴的距离;若不存在,请说明理由.

【答案】(l)![]() ;(2)点
;(2)点![]() 的坐标为
的坐标为![]() ;(3)点
;(3)点![]() 到
到![]() 轴的距离为
轴的距离为![]() .
.
【解析】
(1)根据待定系数法,计算即可.
(2)首先设出P点的坐标,再利用![]() 求解未知数,可得P点的坐标.
求解未知数,可得P点的坐标.
(3)首先求出直线AB的解析式,过点![]() 作
作![]() 轴,垂足为
轴,垂足为![]() ,作
,作![]() 轴交
轴交![]() 于点
于点![]() ,再利用平行证明
,再利用平行证明![]() ,列出方程求解参数,即可的点
,列出方程求解参数,即可的点![]() 到
到![]() 轴的距离.
轴的距离.
(l)因为抛物线![]() 过点
过点![]() ,∴
,∴![]() ,
,
又因为抛物线过点![]() ,
,![]()
∴![]()
解,得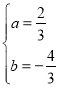
所以,抛物线表达式为![]()
(2)连接![]() ,设点
,设点![]() .
.
则![]()
![]()
![]()
由题意得![]()
∴![]() 或
或![]() (舍)
(舍)
∴![]()
∴点![]() 的坐标为
的坐标为![]() .
.
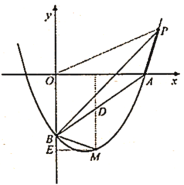
(3)设直线![]() 的表达式为
的表达式为![]() ,因直线
,因直线![]() 过点
过点![]() 、
、
![]() ,
,
∴![]()
解,得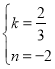
所以![]() 的表达式为
的表达式为![]()
设存在点![]() 满足题意,点
满足题意,点![]() 的坐标为
的坐标为![]() ,过点
,过点![]() 作
作![]() 轴,垂足为
轴,垂足为![]() ,作
,作![]() 轴交
轴交![]() 于点
于点![]() ,则
,则![]() 的坐标为
的坐标为![]() ,
,![]() ,
,![]() .
.
又![]() 轴
轴
∴![]()
又∵![]()
∴![]()
∴![]()
∴![]() .
.
在![]() 中
中
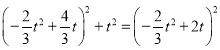
解得:![]()
所以点![]() 到
到![]() 轴的距离为
轴的距离为![]()


科目:初中数学 来源: 题型:
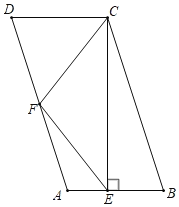
【题目】如图,在四边形ABCD中,AD∥BC,AD=BC=2AB,F是AD的中点,作CE⊥AB,垂足E在线段AB上,连接EF、CF.
(1)若∠ADC=80°,求∠ECF;
(2)求证:∠ECF=∠CEF.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将一副三角板和一张对边平行的纸条按如图的方式摆放,∠A=∠DEF=90°,∠EDF=45°,∠ABC=30°,点E,F均在边AB上,点D在纸条的一边上,若边BC与纸条的另一边重合,则∠α的度数是( )
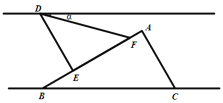
A.15°B.22.5°C.30°D.45°
查看答案和解析>>
科目:初中数学 来源: 题型:
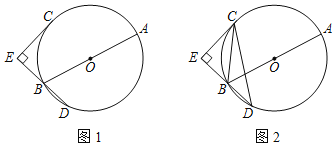
【题目】已知:AB为⊙O的直径,C、D为心⊙O上的点,C是优弧AD的中点,CE⊥DB交DB的延长线于点E.
(1)如图1,判断直线CE与⊙O的位置关系,并说明理由.
(2)如图2,若tan∠BCE=![]() ,连BC、CD,求cos∠BCD的值.
,连BC、CD,求cos∠BCD的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“切实减轻学生课业负担”是我市作业改革的一项重要举措.某中学为了解本校学生平均每天的课外作业时间,随机抽取部分学生进行问卷调查,并将调查结果分为A、B、C、D四个等级,A:1小时以内;B:1小时--1.5小时;C:1.5小时--2小时;D:2小时以上.根据调查结果绘制了如图所示的两种不完整的统计图,请根据图中信息解答下列问题:
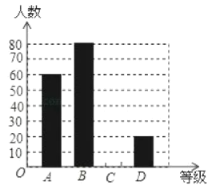
(1)该校共调查了多少名学生?
(2)请将条形统计图补充完整;
(3)在此次调查问卷中,甲、乙两班各有2人平均每天课外作业量都是2小时以上,从这4人中人选2人去参加座谈,用列表或画树状图的方法求选出的2人来自不同班级的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校组织了一次比赛,甲、乙两队各有5人参加比赛,两队每人的比赛成绩(单位:分)如下:
甲队:7,8,9,6,10
乙队:10,9,5,8,8
(1)甲队成绩的中位数是 分,乙队成绩的众数是 分;
(2)计算乙队的平均成绩和方差;
(3)已知甲队成绩的方差为S2甲=2,则成绩波动较大的是 队.
查看答案和解析>>
科目:初中数学 来源: 题型:
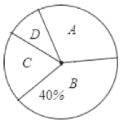
【题目】某校组织学生书法比赛,对参赛作品按A、B、C、D四个等级进行了评定.现随机取部分学生书法作品的评定结果进行分析,并绘制扇形统计图和条形统计图如下:

根据上述信息完成下列问题:
(1)求这次抽取的样本的容量;
(2)请在图②中把条形统计图补充完整;
(3)已知该校这次活动共收到参赛作品750份,请你估计参赛作品达到B级以上(即A级和B级)有多少份?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】现有![]() ,
,![]() 两个不透明的袋子,分别装有3个除颜色外完全相同的小球.其中,
两个不透明的袋子,分别装有3个除颜色外完全相同的小球.其中,![]() 袋装有1个白球,2个红球;
袋装有1个白球,2个红球;![]() 袋装有1个红球,2个白球.
袋装有1个红球,2个白球.
(1)将![]() 袋摇匀,然后从
袋摇匀,然后从![]() 袋中随机摸出一个球,则摸出的小球是红球的概率为______;
袋中随机摸出一个球,则摸出的小球是红球的概率为______;
(2)小王和小周商定了一个游戏规则:从摇匀后的![]() ,
,![]() 两袋中各随机摸出一个球,摸出的这两个球,若颜色相同,则小王获胜;若颜色不同,则小周获胜.请利用概率说明这个游戏规则是否公平.
两袋中各随机摸出一个球,摸出的这两个球,若颜色相同,则小王获胜;若颜色不同,则小周获胜.请利用概率说明这个游戏规则是否公平.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com