
【题目】将一副三角板和一张对边平行的纸条按如图的方式摆放,∠A=∠DEF=90°,∠EDF=45°,∠ABC=30°,点E,F均在边AB上,点D在纸条的一边上,若边BC与纸条的另一边重合,则∠α的度数是( )
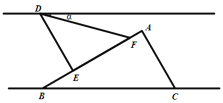
A.15°B.22.5°C.30°D.45°
【答案】A
【解析】
根据直角三角形两锐角互余,求出∠ACB的度数,根据平行线的性质,求出∠DMA的度数,根据多边形内角和公式求出四边形DMAE的度数,分别减去其它三个角,求出∠MDE的度数,最后减去∠FDE的度数,即可解决.
解:如图,延长CA与纸条交于点M,

∵∠BAC=90°,∠ABC=30°,
∴∠ACB=60°,
∵纸条的对边平行,
∴∠ACB+∠DMA=180°,
∴∠DMA=180°-60°=120°,
∵四边形DMAE的内角和=(4-2)×180°=360°,
∴∠MDB=360°-90°-90°-120°=60°,
∵∠EDF=45°,
∴∠α=60°-45°=15°.
故本题答案为:A.


 名师点拨卷系列答案
名师点拨卷系列答案 英才计划期末调研系列答案
英才计划期末调研系列答案科目:初中数学 来源: 题型:
【题目】问题:如图(1),点E、F分别在正方形ABCD的边BC、CD上,∠EAF=45°,试判断BE、EF、FD之间的数量关系.
【发现证明】小聪把△ABE绕点A逆时针旋转90°至△ADG,从而发现EF=BE+FD,请你利用图(1)证明上述结论.
【类比引申】如图(2),四边形ABCD中,∠BAD≠90°,AB=AD,∠B+∠D=180°,点E、F分别在边BC、CD上,则当∠EAF与∠BAD满足 关系时,仍有EF=BE+FD;请证明你的结论.

【探究应用】如图(3),在某公园的同一水平面上,四条通道围成四边形ABCD.已知AB=AD=80米,∠B=60°,∠ADC=120°,∠BAD=150°,道路BC、CD上分别有景点E、F,且AE⊥AD,DF=40(![]() ﹣1)米,现要在E、F之间修一条笔直道路,求这条道路EF的长.(结果取整数,参考数据:
﹣1)米,现要在E、F之间修一条笔直道路,求这条道路EF的长.(结果取整数,参考数据: ![]() =1.41,
=1.41, ![]() =1.73)
=1.73)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为倡导健康环保,自带水杯已成为一种好习惯,某超市销售甲,乙两种型号水杯,进价和售价均保持不变,其中甲种型号水杯进价为25元/个,乙种型号水杯进价为45元/个,下表是前两月两种型号水杯的销售情况:
时间 | 销售数量(个) | 销售收入(元)(销售收入=售价×销售数量) | |
甲种型号 | 乙种型号 | ||
第一月 | 22 | 8 | 1100 |
第二月 | 38 | 24 | 2460 |
(1)求甲、乙两种型号水杯的售价;
(2)第三月超市计划再购进甲、乙两种型号水杯共80个,这批水杯进货的预算成本不超过2600元,且甲种型号水杯最多购进55个,在80个水杯全部售完的情况下设购进甲种号水杯a个,利润为w元,写出w与a的函数关系式,并求出第三月的最大利润.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小吴家准备购买一台电视机,小吴将收集到的某地区A、B、C三种品牌电视机销售情况的有关数据统计如下:
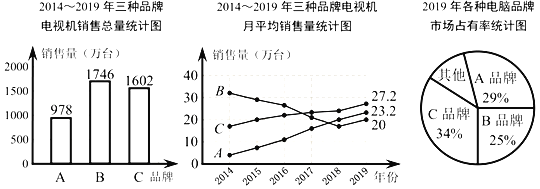
根据上述三个统计图,请解答:
(1)2014~2019年三种品牌电视机销售总量最多的是 品牌,月平均销售量最稳定的是 品牌.
(2)2019年其他品牌的电视机年销售总量是多少万台?
(3)货比三家后,你建议小吴家购买哪种品牌的电视机?说说你的理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
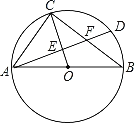
【题目】如图,△ABC内接于⊙O,AB为⊙O的直径,AB=10,AC=6,连结OC,弦AD分别交OC,BC于点E,F,其中点E是AD的中点.
(1)求证:∠CAD=∠CBA.
(2)求OE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
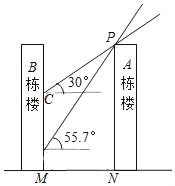
【题目】如图,某小区A栋楼在B栋楼的南侧,两楼高度均为90m,楼间距为MN.春分日正午,太阳光线与水平面所成的角为55.7°,A栋楼在B栋楼墙面上的影高为DM;冬至日正午,太阳光线与水平面所成的角为30°,A栋楼在B栋楼墙面上的影高为CM.已知CD=44.5m.
(1)求楼间距MN;
(2)若B号楼共30层,每层高均为3m,则点C位于第几层?(参考数据:tan30°≈0.58,sin55.7°≈0.83,cos55.7°≈0.56,tan55.7°≈1.47)
查看答案和解析>>
科目:初中数学 来源: 题型:
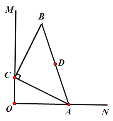
【题目】如图,∠MON =∠ACB = 90°,AC = BC,AB =5,△ABC顶点A、C分别在ON、OM上,点D是AB边上的中点,当点A在边ON上运动时,点C随之在边OM上运动,则OD的最大值为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若二次函数![]() 的图象与
的图象与![]() 轴分别交于点
轴分别交于点![]() 、
、![]() ,且过点
,且过点![]() .
.
(1)求二次函数表达式;
(2)若点![]() 为抛物线上第一象限内的点,且
为抛物线上第一象限内的点,且![]() ,求点
,求点![]() 的坐标;
的坐标;
(3)在抛物线上(![]() 下方)是否存在点
下方)是否存在点![]() ,使
,使![]() ?若存在,求出点
?若存在,求出点![]() 到
到![]() 轴的距离;若不存在,请说明理由.
轴的距离;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
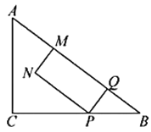
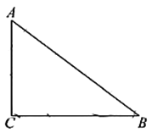
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() .点
.点![]() 从点
从点![]() 出发,以每秒5个单位长度的速度沿
出发,以每秒5个单位长度的速度沿![]() 向终点
向终点![]() 运动,同时点
运动,同时点![]() 从点
从点![]() 出发,以相同的速度沿
出发,以相同的速度沿![]() 向终点
向终点![]() 运动,过点
运动,过点![]() 作
作![]() 于点
于点![]() ,连结
,连结![]() ,以
,以![]() 、
、![]() 为邻边作矩形
为邻边作矩形![]() ,当点
,当点![]() 运动到终点时,整个运动停止,设矩形
运动到终点时,整个运动停止,设矩形![]() 与
与![]() 重叠部分图形的面积为
重叠部分图形的面积为![]() ,点
,点![]() 的运动时间为
的运动时间为![]() 秒.
秒.
(1)①![]() 的长为 ;
的长为 ;
②用含![]() 的代数式表示线段
的代数式表示线段![]() 的长为 ;
的长为 ;
(2)当![]() 的长度为10时,求
的长度为10时,求![]() 的值;
的值;
(3)求![]() 与
与![]() 的函数关系式;
的函数关系式;
(4)当过点![]() 和点
和点![]() 的直线垂直于
的直线垂直于![]() 的一边时,直接写出
的一边时,直接写出![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com