
【题目】如图,已知抛物线与![]() 轴交于
轴交于![]() ,
,![]() 点,与
点,与![]() 轴交于点
轴交于点![]() ,抛物线的顶点为
,抛物线的顶点为![]() ,连接
,连接![]() .
.
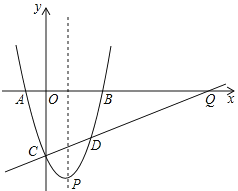
(1)求此抛物线的表达式;
(2)在抛物线上找一点![]() ,使得
,使得![]() 与
与![]() 垂直,且直线
垂直,且直线![]() 与
与![]() 轴交于点
轴交于点![]() ,求点
,求点![]() 的坐标;
的坐标;
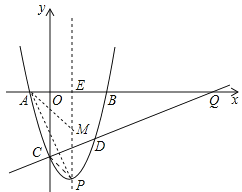
(3)抛物线对称轴上是否存在一点![]() ,使得
,使得![]() ,若存在,求出
,若存在,求出![]() 点坐标;若不存在,请说明理由.
点坐标;若不存在,请说明理由.
【答案】(1)![]() (2)
(2)![]() (3)存在;
(3)存在;![]() 或
或![]()
【解析】
(1)利用交点式将抛物线与x轴交于A(-1,0)、B(3,0)两点,代入y=a(x-x1)(x-x2),求出二次函数解析式即可;
(2)利用△QOC∽△COA,得出QO的长度,得出Q点的坐标,再求出直线QC的解析式,将两函数联立求出交点坐标即可;
(3)首先求出二次函数顶点坐标,由S四边形AEPC=S四边形OEPC+S△AOC以及S四边形AEPC=S△AEP+S△ACP,得出使得S△MAP=3S△ACP的点M的坐标.
解:(1)设此抛物线的表达式为![]()
![]() 抛物线与
抛物线与![]() 轴交于点
轴交于点![]()
![]()
![]() 抛物线与
抛物线与![]() 轴交于
轴交于![]() ,
,![]() 两点
两点
![]()
解得![]()
此抛物线的表达式为![]()
(2)![]() ,
,![]() ,
,
![]() ,
,![]()
![]() ,
,![]()
![]() 轴,
轴,
![]() ,
,![]() ,
,
![]() ,
,
![]()
![]()
即![]()
![]()
又![]() 点
点![]() 在
在![]() 轴的正半轴上,
轴的正半轴上,
![]()
设直线![]() 的表达式为
的表达式为![]()
则![]()
解得
![]() 直线
直线![]() 的表达式为
的表达式为![]() :
:
![]() 点
点![]() 是抛物线与直线
是抛物线与直线![]() 的交点
的交点
![]()
解得![]() ,
,![]() (不合题意舍去)
(不合题意舍去)
此时![]()
![]()
(3)对称轴;![]()
此时![]()
![]()
点![]() 在直线
在直线![]() 上,
上,
设![]() ,连接
,连接![]() 、
、![]() 、
、![]()
直线![]() 与
与![]() 轴交于点
轴交于点![]() ,
,
![]() ,
,![]()
则![]()
![]()
又![]()
![]() ,
,
![]()
![]()
![]() ,
,
![]() ,
,![]() ,
,![]() .
.
故对称轴上存在点![]() 使
使![]() ,点
,点![]() 的坐标为
的坐标为![]() 或
或![]() .
.
【点晴】
本题主要考查了二次函数的综合应用,二次函数的综合应用是初中阶段的重点题型,特别注意利用数形结合是这部分考查的重点,也是难点.


科目:初中数学 来源: 题型:
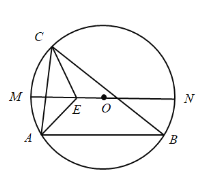
【题目】如图,![]() 是
是![]() 的直径,弦
的直径,弦![]() 点
点![]() 是直径
是直径![]() 上方半圆上的动点(包括端点
上方半圆上的动点(包括端点![]() 和
和![]() 的平分线相交于点E,当点
的平分线相交于点E,当点![]() 从点
从点![]() 运动到点
运动到点![]() 时,则
时,则![]() 两点的运动路径长的比值是( )
两点的运动路径长的比值是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 为
为![]() 的直径,
的直径,![]() 于点
于点 ![]() ,
,![]() 是
是![]() 上一点,且
上一点,且![]() ,延长
,延长![]() 至点
至点![]() ,连接
,连接![]() ,使
,使![]() ,延长
,延长![]() 与
与![]() 交于点
交于点![]() ,连结
,连结![]() ,
,![]() .
.
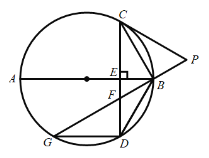
(1)连结![]() ,求证:
,求证:![]() ;
;
(2)求证:![]() 是
是![]() 的切线;
的切线;
(3)若![]() ,且
,且![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个不透明的口袋中有标号为1,2,3,4的四个小球,除数字不同外,小球没有任何区别,摸球前先搅拌均匀,每次摸一个球
(1)摸出一个球,摸到标号为偶数的概率为 .
(2)从袋中不放回地摸两次,用列表或树状图求出两球标号数字为一奇一偶的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
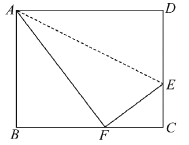
【题目】如图,折叠矩形ABCD的一边AD,使点D落在BC边的点F处,已知折痕AE=5![]() cm, 且tan∠EFC=
cm, 且tan∠EFC=![]() ,那么矩形ABCD的周长_____________cm.
,那么矩形ABCD的周长_____________cm.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知反比例函数![]() (k≠8)的图像经过点A(1,6).
(k≠8)的图像经过点A(1,6).
(1)求k的值;
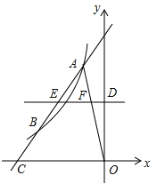
(2)如图,过点A作直线AC与函数![]() 的图像交于点B,与x轴交于点C,且AB=2BC,求直线AC的解析式;
的图像交于点B,与x轴交于点C,且AB=2BC,求直线AC的解析式;
(3)在(2)的条件下,连接OA,过y轴的正半轴上的一点D作直线DE∥x轴,分别交线段AC、OA于点E、F,若△AEF的面积为![]() ,求点D的坐标.
,求点D的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数![]() 与一次函数
与一次函数![]() ,
,
(1)求证:对任意的实数![]() ,函数
,函数![]() 与
与![]() 的图象总有两个交点;
的图象总有两个交点;
(2)设![]() 与
与![]() 的图象相交于
的图象相交于![]() 两点,
两点,![]() 的图象与
的图象与![]() 轴相交于点
轴相交于点![]() ,记
,记![]() 与
与![]() 的面积分别为
的面积分别为![]() (
(![]() 为坐标原点),求证:
为坐标原点),求证:![]() 总是定值;
总是定值;
(3)对于二次函数![]() ,是否存在实数
,是否存在实数![]() ,使得当
,使得当![]() 时,恰好有
时,恰好有![]() ,若存在,请求出
,若存在,请求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
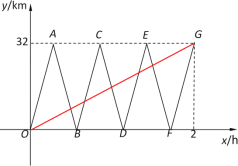
【题目】某观光湖风景区,一观光轮与一巡逻艇同时从甲码头出发驶往乙码头,巡逻艇匀速往返于甲、乙两个码头之间,当观光轮到达乙码头时,巡逻艇也同时到达乙码头.设出发x h后,观光轮、巡逻艇离甲码头的距离分别为y1 km、y2 km.图中的线段OG、折线OABCDEFG分别表示y1、y2 与x之间的函数关系.
(1)观光轮的速度是 km/h,巡逻艇的速度是 km/h;
(2)求整个过程中观光轮与巡逻艇的最大距离;
(3)求整个过程中观光轮与巡逻艇相遇的最短时间间隔.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,PB为⊙O的切线,B为切点,直线PO交⊙于点E、F,过点B作PO的垂线BA,垂足为点D,交⊙O于点A,延长AO与⊙O交于点C,连接BC,AF.
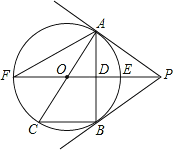
(1)求证:直线PA为⊙O的切线;
(2)试探究线段EF、OD、OP之间的等量关系,并加以证明;
(3)若BC=6,tan∠F=![]() ,求cos∠ACB的值和线段PE的长.
,求cos∠ACB的值和线段PE的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com