
【题目】如图,![]() 为
为![]() 的直径,
的直径,![]() 于点
于点 ![]() ,
,![]() 是
是![]() 上一点,且
上一点,且![]() ,延长
,延长![]() 至点
至点![]() ,连接
,连接![]() ,使
,使![]() ,延长
,延长![]() 与
与![]() 交于点
交于点![]() ,连结
,连结![]() ,
,![]() .
.
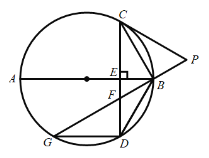
(1)连结![]() ,求证:
,求证:![]() ;
;
(2)求证:![]() 是
是![]() 的切线;
的切线;
(3)若![]() ,且
,且![]() ,求
,求![]() 的值.
的值.
【答案】(1)见解析;(2)见解析;(3)![]()
【解析】
(1)证得![]() ,根据AAS可证得△BCD≌△DGB,从而结论得证;
,根据AAS可证得△BCD≌△DGB,从而结论得证;
(2)连接OC,由于![]() ,
,![]() ,从而可得
,从而可得![]() ,又因为PC=PF,从而可知
,又因为PC=PF,从而可知![]() ,由于AB⊥CD,∠COB+∠OCE=90°,所以
,由于AB⊥CD,∠COB+∠OCE=90°,所以![]() ,从而得证;
,从而得证;
(3)连接![]() ,证得
,证得![]() ,所以tanG=tan∠BCD=
,所以tanG=tan∠BCD=![]() ,设
,设![]() ,则
,则![]() ,
,![]() ,从而可求出BE,CE的长度,再由勾股定理可知BC的长度,证明
,从而可求出BE,CE的长度,再由勾股定理可知BC的长度,证明![]() ,得出
,得出![]() ,从而可求出FD.
,从而可求出FD.
解:(1)证明:∵![]() ,∴
,∴![]() ,
,
∵![]() ∴
∴![]()
∵![]() ∴
∴![]()
∴![]()
(2)证明:连接![]() .
.
∵![]() ∴
∴![]()
∵![]() ,∴
,∴![]() ,
,
∵![]() ,∴
,∴![]() ,∴
,∴![]() ,
,
∵![]() ,∴
,∴![]() ,
,
∴![]() ,即
,即![]() ,
,
∴![]() ,
,
∴![]() 是圆
是圆![]() 的切线.
的切线.
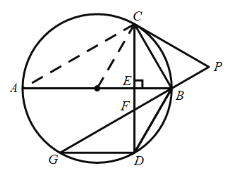
(3)连接![]() ,∵直径
,∵直径![]() 弦
弦![]() 于
于![]() ,
,
∴![]() ,
,![]() ,∴
,∴![]() ,
,
∵![]() ,∴
,∴![]() ,
,![]()
设![]() ,则
,则![]() ,
,![]()
∵![]()
∴![]()
解得![]() ,
,
∴![]() ,
,![]()
∴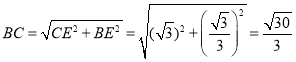 ,
,![]()
∴![]() ,
,
∵![]() ,
,![]() ,
,
∴![]()
∵![]()
∴![]() ,
,
![]()
即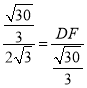 ,
,
∴![]()


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】现有![]() ,
,![]() 两个不透明的袋子,分别装有3个除颜色外完全相同的小球.其中,
两个不透明的袋子,分别装有3个除颜色外完全相同的小球.其中,![]() 袋装有1个白球,2个红球;
袋装有1个白球,2个红球;![]() 袋装有1个红球,2个白球.
袋装有1个红球,2个白球.
(1)将![]() 袋摇匀,然后从
袋摇匀,然后从![]() 袋中随机摸出一个球,则摸出的小球是红球的概率为______;
袋中随机摸出一个球,则摸出的小球是红球的概率为______;
(2)小王和小周商定了一个游戏规则:从摇匀后的![]() ,
,![]() 两袋中各随机摸出一个球,摸出的这两个球,若颜色相同,则小王获胜;若颜色不同,则小周获胜.请利用概率说明这个游戏规则是否公平.
两袋中各随机摸出一个球,摸出的这两个球,若颜色相同,则小王获胜;若颜色不同,则小周获胜.请利用概率说明这个游戏规则是否公平.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市一研究机构为了了解![]() 岁年龄段市民对创建文明城市的关注程度,随机选取了
岁年龄段市民对创建文明城市的关注程度,随机选取了![]() 名年龄在该范围内的市民进行了调查,并将收集到的数据制成了尚不完整的频数分布表、频数分布直方图和扇形统计图,如下所示:
名年龄在该范围内的市民进行了调查,并将收集到的数据制成了尚不完整的频数分布表、频数分布直方图和扇形统计图,如下所示:
组别 | 年龄段 | 频数(人数) |
第 |
|
|
第 |
|
|
第 |
|
|
第 |
|
|
第 |
|
|
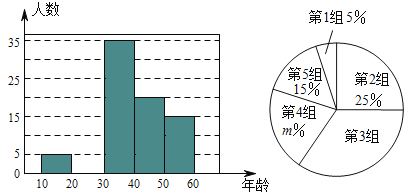
(1)请直接写出![]() ,第
,第![]() 组人数在扇形统计图中所对应的圆心角是 度;
组人数在扇形统计图中所对应的圆心角是 度;
(2)请补全上面的频数分布直方图:
(3)假设该市现有![]() 岁的市民
岁的市民![]() 万人,问
万人,问![]() 岁年龄段的关注创建文明城市的人数约有多少?
岁年龄段的关注创建文明城市的人数约有多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】第5代移动通信技术简称5G,某地已开通5G业务,经测试5G下载速度是4G下载速度的15倍,小明和小强分别用5G与4G下载一部600兆的公益片,小明比小强所用的时间快140秒,求该地4G与5G的下载速度分别是每秒多少兆?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】PM2.5是指大气中直径小于或等于2.5μm(0.0000025m)的颗粒物,含有大量有毒、有害物质,也称可入肺颗粒物.将0.0000025用科学记数法表示为
A.25×10﹣7B.2.5×10﹣6C.0.25×10﹣5D.2.5×106
查看答案和解析>>
科目:初中数学 来源: 题型:
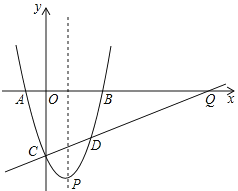
【题目】如图,已知抛物线与![]() 轴交于
轴交于![]() ,
,![]() 点,与
点,与![]() 轴交于点
轴交于点![]() ,抛物线的顶点为
,抛物线的顶点为![]() ,连接
,连接![]() .
.
(1)求此抛物线的表达式;
(2)在抛物线上找一点![]() ,使得
,使得![]() 与
与![]() 垂直,且直线
垂直,且直线![]() 与
与![]() 轴交于点
轴交于点![]() ,求点
,求点![]() 的坐标;
的坐标;
(3)抛物线对称轴上是否存在一点![]() ,使得
,使得![]() ,若存在,求出
,若存在,求出![]() 点坐标;若不存在,请说明理由.
点坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
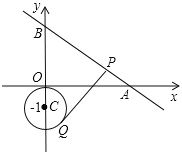
【题目】如图,直线![]() 与
与![]() 轴,
轴,![]() 轴分别交于点
轴分别交于点![]() 、
、![]() ;点
;点![]() 是以
是以![]() 为圆心,1为半径的圆上一动点,过Q点的切线交线段AB于点P,当线段PQ取最小值时,P点的坐标是__________.
为圆心,1为半径的圆上一动点,过Q点的切线交线段AB于点P,当线段PQ取最小值时,P点的坐标是__________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com