
【题目】如图,函数![]() (
(![]() ,
,![]() ,
,![]() 为常数,且
为常数,且![]() )经过点
)经过点![]() 、
、![]() ,且
,且![]() ,下列结论:
,下列结论:
①![]() ;②
;②![]() ;③若点
;③若点![]() ,
,![]() 在抛物线上,则
在抛物线上,则![]() ;④
;④![]() .其中结论正确的有( )个
.其中结论正确的有( )个
A.1B.2C.3D.4
【答案】C
【解析】
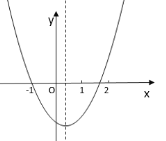
据题意画出抛物线的大致图象,利用函数图象,由抛物线开口方向得a>0,由抛物线的对称轴位置得b<0,由抛物线与y轴的交点位置得c<0,于是可对①进行判断;由于抛物线过点(﹣1,0)和(m,0),且1<m<2,根据抛物线的对称性和对称轴方程得到![]() ,则可对②进行判断;利用点A(﹣2,y1)和点B(2,y2)到对称轴的距离的大小可对③进行判断;根据抛物线上点的坐标特征得a﹣b+c=0,am2+bm+c=0,两式相减得am2﹣a+bm+b=0,然后把等式左边分解后即可得到a(m﹣1)+b=0,则可对④进行判断.
,则可对②进行判断;利用点A(﹣2,y1)和点B(2,y2)到对称轴的距离的大小可对③进行判断;根据抛物线上点的坐标特征得a﹣b+c=0,am2+bm+c=0,两式相减得am2﹣a+bm+b=0,然后把等式左边分解后即可得到a(m﹣1)+b=0,则可对④进行判断.
∵抛物线开口向上,
∴a>0,
∵抛物线的对称轴在y轴的右侧,
∴b<0,
∵抛物线与y轴的交点在x轴下方,
∴c<0,
∴abc>0,
∴①的结论正确;
∵抛物线过点(﹣1,0)和(m,0),且1<m<2,
∴对称轴![]()
∴![]() ,故②的结论正确;
,故②的结论正确;
∵点A(﹣2,y1)到对称轴的距离比点B(2,y2)到对称轴的距离远,
∴y1>y2,
∴③的结论错误;
∵抛物线过点(﹣1,0),(m,0),
∴a﹣b+c=0,am2+bm+c=0,
∴am2﹣a+bm+b=0,
a(m+1)(m﹣1)+b(m+1)=0,
∴a(m﹣1)+b=0,
∴④的结论正确;
综上所述①②④结论正确
故选:C.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】为庆祝![]() 年中国航天日,发扬中国航天精神,激发青少年崇尚科学探索未知和敢于创新的热情,某校举行班级歌咏比赛,歌曲有:《祖国不会忘记》,《飞天》,《仰望星空》(分别用字母
年中国航天日,发扬中国航天精神,激发青少年崇尚科学探索未知和敢于创新的热情,某校举行班级歌咏比赛,歌曲有:《祖国不会忘记》,《飞天》,《仰望星空》(分别用字母![]() ,
,![]() ,
,![]() 依次表示这三首歌曲).比赛时,将
依次表示这三首歌曲).比赛时,将![]() ,
,![]() ,
,![]() 这三个字母分别写在
这三个字母分别写在![]() 张无差别不透明的卡片正面上,洗匀后正面向下放在桌面上,九(1)班班长先从中随机抽取一张卡片放回后洗匀,再由九(2)班班长从中随机抽取一张卡片,进行歌咏比赛.
张无差别不透明的卡片正面上,洗匀后正面向下放在桌面上,九(1)班班长先从中随机抽取一张卡片放回后洗匀,再由九(2)班班长从中随机抽取一张卡片,进行歌咏比赛.
(1)九(1)班抽中歌曲《祖国不会忘记》的概率是______;
(2)试用画树状图或列表的方法表示所有可能的结果,并求出九(1)班和九(2)班抽中不同歌曲的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,![]() 是
是![]() 的直径,
的直径,![]() 为
为![]() 上不同于
上不同于![]() 的两点,连接
的两点,连接![]() 且
且![]() 过点
过点![]() 作
作![]() 垂足为
垂足为![]() 直线
直线![]() 与
与![]() 相交于点
相交于点![]() .
.
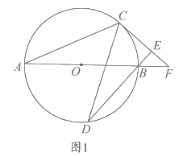
(1)求证:![]() 是
是![]() 的切线;
的切线;
(2)若![]()
①求直径![]() 的长;
的长;
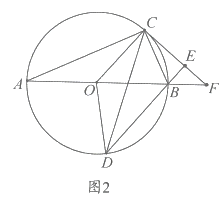
②如图2所示,连接![]() 直接写出
直接写出![]() 的面积与四边形
的面积与四边形![]() 的面积的比值 .
的面积的比值 .
查看答案和解析>>
科目:初中数学 来源: 题型:
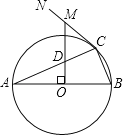
【题目】如图,AB是⊙O的直径,点C为⊙O上一点,CN为⊙O的切线,OM⊥AB于点O,分别交AC、CN于D、M两点.
(1)求证:MD=MC;
(2)若⊙O的半径为5,AC=4![]() ,求MC的长.
,求MC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】北京和上海都有检测新冠肺炎病毒的仪器可供外地使用,其中北京有![]() 台,上海有
台,上海有![]() 台.
台.
(1)已知武汉需要![]() 台,温州需要
台,温州需要![]() 台,从北京、上海将仪器运往武汉、温州的费用如下表所示,有关部门计划用
台,从北京、上海将仪器运往武汉、温州的费用如下表所示,有关部门计划用![]() 元运送这些仪器.请你设计一种运送方案,使武汉、温州能得到所需仪器,而且运费正好够用.
元运送这些仪器.请你设计一种运送方案,使武汉、温州能得到所需仪器,而且运费正好够用.
(2)为了节约运送资金,中央防控工作组统一调配仪器,分配到温州的仪器不能超过![]() 台,则如何调配?
台,则如何调配?
终点 起点 | 温州 | 武汉 |
北京 |
|
|
上海 |
|
|
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 为
为![]() 的直径,
的直径,![]() 于点
于点 ![]() ,
,![]() 是
是![]() 上一点,且
上一点,且![]() ,延长
,延长![]() 至点
至点![]() ,连接
,连接![]() ,使
,使![]() ,延长
,延长![]() 与
与![]() 交于点
交于点![]() ,连结
,连结![]() ,
,![]() .
.
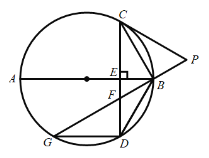
(1)连结![]() ,求证:
,求证:![]() ;
;
(2)求证:![]() 是
是![]() 的切线;
的切线;
(3)若![]() ,且
,且![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1是自动卸货汽车卸货时的状态图,图2是其示意图.汽车的车厢采用液压机构、车厢的支撑顶杆BC的底部支撑点B在水平线AD的下方,AB与水平线AD之间的夹角是5°,卸货时,车厢与水平线AD成60°,此时AB与支撑顶杆BC的夹角为45°,若AC=2米,求BC的长度.(结果保留一位小数)
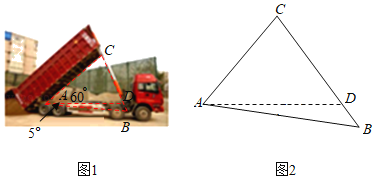
(参考数据:sin65°≈0.91,cos65°≈0.42,tan65°≈2.14,sin70°≈0.94,cos70°≈0.34,tan70°≈2.75,![]() ≈1.41)
≈1.41)
查看答案和解析>>
科目:初中数学 来源: 题型:
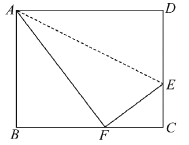
【题目】如图,折叠矩形ABCD的一边AD,使点D落在BC边的点F处,已知折痕AE=5![]() cm, 且tan∠EFC=
cm, 且tan∠EFC=![]() ,那么矩形ABCD的周长_____________cm.
,那么矩形ABCD的周长_____________cm.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠C=90°,AC=2cm,AB=4cm.点P从点A出发,沿AB以1cm/s的速度向终点B运动.当点P与点A、B不重合时,过点P作PQ⊥AB交射线AC于点Q,以AP,AQ为邻边向上作平行四边形APMQ.设点P的运动时间为x(s),解答下列问题.
(1)∠A= °;
(2)当点M在BC上时,x的值为 ;
(3)设平行四边形APMQ与△ABC的重叠部分图形的面积为y(cm2),求y与x之间的函数关系式;
(4)整个运动过程中,直接写出△ABM为直角三角形时x的值.
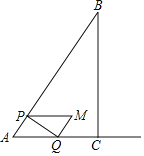
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com