
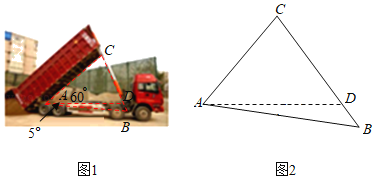
【题目】如图1是自动卸货汽车卸货时的状态图,图2是其示意图.汽车的车厢采用液压机构、车厢的支撑顶杆BC的底部支撑点B在水平线AD的下方,AB与水平线AD之间的夹角是5°,卸货时,车厢与水平线AD成60°,此时AB与支撑顶杆BC的夹角为45°,若AC=2米,求BC的长度.(结果保留一位小数)
(参考数据:sin65°≈0.91,cos65°≈0.42,tan65°≈2.14,sin70°≈0.94,cos70°≈0.34,tan70°≈2.75,![]() ≈1.41)
≈1.41)
【答案】所求BC的长度约为2.6米.
【解析】
过点A作AE⊥BC于点E,先求出∠C,再运用锐角三角函数关系的知识求得CE和AE,然后再说明△AEB是等腰直角三角形得到AE=BE,最后根据BC=BE+CE解答即可.
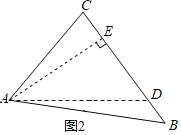
解:如图,过点A作AE⊥BC于点E,
∵在Rt△ACE中,∠C=180°﹣65°﹣45°=70°,
∴cosC=cos70°=![]() ,即CE=AC×cos70°≈2×0.34=0.68,
,即CE=AC×cos70°≈2×0.34=0.68,
sinC=sin70°=![]() ,AE=AC×sin70°≈2×0.94=1.88,
,AE=AC×sin70°≈2×0.94=1.88,
又∵在Rt△AEB中,∠ABC=45°,
∴△AEB是等腰直角三角形
∴AE=BE,
∴BC=BE+CE=0.68+1.88=2.56≈2.6,
答:所求BC的长度约为2.6米.


科目:初中数学 来源: 题型:
【题目】新冠病毒潜伏期较长,能通过多种渠道传播,以在生活中就要做好最基本的防护:在公共区域和陌生人保持距离,勤洗手,出门戴口罩某区中小学陆续复学后,为了提高同学们的防疫意识,决定组织防疫知识竞赛活动,评出一、二三等奖各若干名,并分别发给洗手液、温度计和口罩作为奖品.
(1)如果温度计的单价比口罩的单价多![]() 元,购买洗手液
元,购买洗手液![]() 瓶和口罩
瓶和口罩![]() 个共需
个共需![]() 元;购买
元;购买![]() 瓶洗手液比购买
瓶洗手液比购买![]() 支温度计多花
支温度计多花![]() 元,求洗手液、温度计和口罩的单价各是多少元?
元,求洗手液、温度计和口罩的单价各是多少元?
(2)已知本次竞赛活动获得三等奖的人数是获得二等奖人数的![]() 倍,且获得一等奖的人数不超过获奖总人数的五分之一,如果购买这三种奖品的总费用为
倍,且获得一等奖的人数不超过获奖总人数的五分之一,如果购买这三种奖品的总费用为![]() 元,求本次竞赛活动获得一、二、三等奖各有多少人.
元,求本次竞赛活动获得一、二、三等奖各有多少人.
查看答案和解析>>
科目:初中数学 来源: 题型:
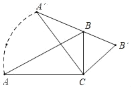
【题目】如图,在Rt△ABC中,∠ACB=90°,∠A=30°,AB=6,将Rt△ABC绕点C顺时针旋转,使斜边A′B′过B点,则线段CA扫过的面积为_____.(结果保留根号和π)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列结论:①b2﹣4ac>0;②abc<0;③4a+b=0;④4a﹣2b+c>0.其中正确结论的个数是( )
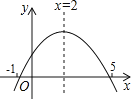
A.4B.3C.2D.1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】PM2.5是指大气中直径小于或等于2.5μm(0.0000025m)的颗粒物,含有大量有毒、有害物质,也称可入肺颗粒物.将0.0000025用科学记数法表示为
A.25×10﹣7B.2.5×10﹣6C.0.25×10﹣5D.2.5×106
查看答案和解析>>
科目:初中数学 来源: 题型:
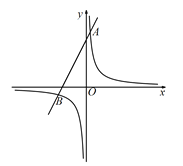
【题目】如图,在平面系中,一次函数![]() 的图像经过定点A,反比例函数
的图像经过定点A,反比例函数![]() 的图像经过点A,且与一次函数
的图像经过点A,且与一次函数![]() 的图像相交于点B(
的图像相交于点B(![]() ,m).
,m).
(1)求m、a的值;
(2)设横坐标为n的点P在反比例函数图象的第三象限上,且在点B右侧,连接AP、BP,△ABP的面积为12,求代数式![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
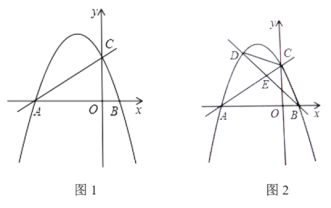
【题目】如图1,在平面直角坐标系中,直线y=![]() x+2与x轴交于点A,与y轴交于点C,二次函数y=
x+2与x轴交于点A,与y轴交于点C,二次函数y=![]() x2+bx+c的图像经过A、C两点,与x轴的另一交点为点B.
x2+bx+c的图像经过A、C两点,与x轴的另一交点为点B.
(1)求二次函数的表达式;
(2)当m≤x≤m1时,二次函数y![]() x2bxc的最大值为2m,求m的值;
x2bxc的最大值为2m,求m的值;
(3)如图2,点D为直线AC上方二次函数图像上一动点,连接BC、CD,设直线BD交线段AC于点E,△CDE的面积为S1,△BCE的面积为S2,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了检测疫情期间的学习效果,某班依据学校要求进行了测试,并将成绩分成![]() 五个等级,依据相关数据绘制如下不完整统计图表如下,请解答问题:
五个等级,依据相关数据绘制如下不完整统计图表如下,请解答问题:
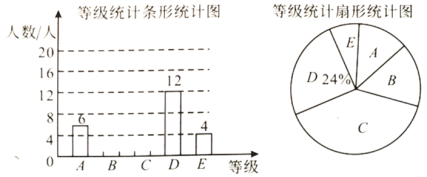
(1)该班参与测试的人数为________;
(2)![]() 等级的人数之比为
等级的人数之比为![]() ,依据数据补全统计图;
,依据数据补全统计图;
(3)扇形图中,![]() 等级人数所对应的扇形图中的圆心角为________;
等级人数所对应的扇形图中的圆心角为________;
(4)若全年级共有1400人,请估计年级部测试等级在![]() 等级以上(包括
等级以上(包括![]() 级)的学生人数.
级)的学生人数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com