
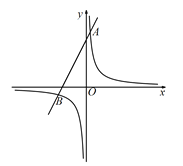
【题目】如图,在平面系中,一次函数![]() 的图像经过定点A,反比例函数
的图像经过定点A,反比例函数![]() 的图像经过点A,且与一次函数
的图像经过点A,且与一次函数![]() 的图像相交于点B(
的图像相交于点B(![]() ,m).
,m).
(1)求m、a的值;
(2)设横坐标为n的点P在反比例函数图象的第三象限上,且在点B右侧,连接AP、BP,△ABP的面积为12,求代数式![]() 的值.
的值.
科目:初中数学 来源: 题型:
【题目】绘制函数![]() 的图象,我们经历了如下过程:确定自变量
的图象,我们经历了如下过程:确定自变量![]() 的取值范围是
的取值范围是![]() ;列表-描点--连线,得到该函数的图象如图所示
;列表-描点--连线,得到该函数的图象如图所示
| ... |
|
|
|
|
|
|
|
|
|
|
|
|
|
| ... |
| ... |
|
|
|
|
|
|
|
|
|
|
|
|
|
| ... |
观察函数图象,回答下列问题:
(1)函数图象在第 象限;
(2)函数图象的对称性是
B.只是轴对称图形,不是中心对称图形
A.既是轴对称图形,又是中心对称图形
D.既不是轴对称图形,也不是中心对称图形
C.不是轴对称图形,而是中心对称图形
(3)在![]() 时,当
时,当![]() 时,函数
时,函数![]() 有最 (大,小)值,且这个最值等于
有最 (大,小)值,且这个最值等于
在![]() 时,当
时,当![]() 时,函数
时,函数![]() 有最 (大,小)值,且这个最值等于
有最 (大,小)值,且这个最值等于
(4)方程![]() 是否有实数解?说明
是否有实数解?说明
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】北京和上海都有检测新冠肺炎病毒的仪器可供外地使用,其中北京有![]() 台,上海有
台,上海有![]() 台.
台.
(1)已知武汉需要![]() 台,温州需要
台,温州需要![]() 台,从北京、上海将仪器运往武汉、温州的费用如下表所示,有关部门计划用
台,从北京、上海将仪器运往武汉、温州的费用如下表所示,有关部门计划用![]() 元运送这些仪器.请你设计一种运送方案,使武汉、温州能得到所需仪器,而且运费正好够用.
元运送这些仪器.请你设计一种运送方案,使武汉、温州能得到所需仪器,而且运费正好够用.
(2)为了节约运送资金,中央防控工作组统一调配仪器,分配到温州的仪器不能超过![]() 台,则如何调配?
台,则如何调配?
终点 起点 | 温州 | 武汉 |
北京 |
|
|
上海 |
|
|
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1是自动卸货汽车卸货时的状态图,图2是其示意图.汽车的车厢采用液压机构、车厢的支撑顶杆BC的底部支撑点B在水平线AD的下方,AB与水平线AD之间的夹角是5°,卸货时,车厢与水平线AD成60°,此时AB与支撑顶杆BC的夹角为45°,若AC=2米,求BC的长度.(结果保留一位小数)
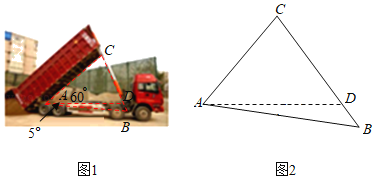
(参考数据:sin65°≈0.91,cos65°≈0.42,tan65°≈2.14,sin70°≈0.94,cos70°≈0.34,tan70°≈2.75,![]() ≈1.41)
≈1.41)
查看答案和解析>>
科目:初中数学 来源: 题型:
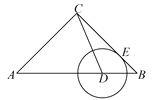
【题目】如图,△ABC中,AC=BC=4,∠ACB=90°,D为边AB上一动点(不与A、B重合),⊙D与BC切于E点,E点关于CD的对称点F在△ABC的一边上,则BD=______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,折叠矩形ABCD的一边AD,使点D落在BC边的点F处,已知折痕AE=5![]() cm, 且tan∠EFC=
cm, 且tan∠EFC=![]() ,那么矩形ABCD的周长_____________cm.
,那么矩形ABCD的周长_____________cm.
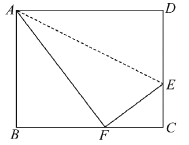
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图![]() ,将一张矩形纸片
,将一张矩形纸片![]() 沿着对角线
沿着对角线![]() 向上折叠,顶点
向上折叠,顶点![]() 落到点
落到点![]() 处,
处,![]() 交
交![]() 于点
于点![]()
(1)求证:![]() 是等腰三角形;
是等腰三角形;
(2)如图![]() ,过点
,过点![]() 作
作![]() ,交
,交![]() 于点
于点![]() ,连接
,连接![]() 交
交![]() 于点
于点![]()
①判断四边形![]() 的形状,并说明理由;
的形状,并说明理由;
②若![]() ,
,![]() ,求
,求![]() 的长
的长
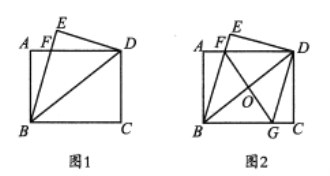
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com