
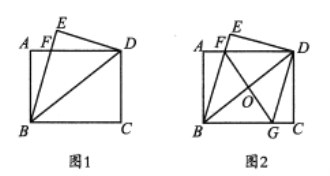
【题目】如图![]() ,将一张矩形纸片
,将一张矩形纸片![]() 沿着对角线
沿着对角线![]() 向上折叠,顶点
向上折叠,顶点![]() 落到点
落到点![]() 处,
处,![]() 交
交![]() 于点
于点![]()
(1)求证:![]() 是等腰三角形;
是等腰三角形;
(2)如图![]() ,过点
,过点![]() 作
作![]() ,交
,交![]() 于点
于点![]() ,连接
,连接![]() 交
交![]() 于点
于点![]()
①判断四边形![]() 的形状,并说明理由;
的形状,并说明理由;
②若![]() ,
,![]() ,求
,求![]() 的长
的长
【答案】(1)见解析;(2)①菱形,见解析,②![]()
【解析】
(1)证明△BDF是等腰三角形,可证明BF=DF,可通过证明∠EBD=∠FDB实现,利用折叠的性质和平行线的性质解决;
(2)①先判断四边形BFDG是平行四边形,再由(1)BF=FD得到结论;
②要求FG的长,可先求出OF的长,在Rt△BFO中,BO可由AB、AD的长及菱形的性质求得,解决问题的关键是求出BF的长.在Rt△BFA中,知AB=6、AF+BF=AD=8,可求出BF的长,问题得以解决.
(1)如图1,∵四边形ABCD是矩形,
∴AD∥BC,
∴∠ADB=∠CBD,
由折叠的性质可知:∠EBD=∠CBD,∴∠ADB=∠EBD,
∴BF=FD
∴△BDF是等腰三角形;
(2)如图2,
① 四边形![]() 是菱形.
是菱形.
理由:∵FD∥BG,DG∥BE,
∴四边形BFDG是平行四边形,
又∵BF=DF,
∴四边形BFDG是菱形;
② 设AF=x,则FD=8x,
∴由折叠性质得BF=FD=8x,
在Rt△ABF中,由勾股定理得:![]()
解得:![]() ,
,
∴FD=![]() ,
,
在Rt△ABD中,∵AB=6,AD=8,
∴BD=10
∵四边形BFDG是菱形,
∴OD=![]() BD=5,FO=
BD=5,FO=![]() FG,FG⊥BD,
FG,FG⊥BD,
在Rt△ODF中,
∵![]() ,即
,即![]() ,
,
∴FO=![]() ,
,
∴FG=2FO=![]() ,
,
故答案为:![]() .
.
![]() 的长为
的长为![]() .
.


科目:初中数学 来源: 题型:
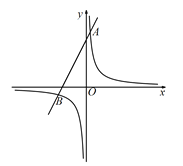
【题目】如图,在平面系中,一次函数![]() 的图像经过定点A,反比例函数
的图像经过定点A,反比例函数![]() 的图像经过点A,且与一次函数
的图像经过点A,且与一次函数![]() 的图像相交于点B(
的图像相交于点B(![]() ,m).
,m).
(1)求m、a的值;
(2)设横坐标为n的点P在反比例函数图象的第三象限上,且在点B右侧,连接AP、BP,△ABP的面积为12,求代数式![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(概念认识)
若以圆的直径的两个端点和圆外一点为顶点的三角形是等腰三角形,则圆外这一点称为这个圆的径等点.
(数学理解)
(1)如图①,AB是⊙O的直径,点P为⊙O外一点,连接AP交⊙O于点C,PC=AC.
求证:点P为⊙O的径等点.

(2)已知AB是⊙O的直径,点P为⊙O的径等点,连接AP交⊙O于点C,若PC=2AC.求![]() 的值.
的值.
(问题解决)
(3)如图②,已知AB是⊙O的直径.若点P为⊙O的径等点,连接AP交⊙O于点C,PC=3AC.利用直尺和圆规作出所有满足条件的点P.(保留作图痕迹,不写作法)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了检测疫情期间的学习效果,某班依据学校要求进行了测试,并将成绩分成![]() 五个等级,依据相关数据绘制如下不完整统计图表如下,请解答问题:
五个等级,依据相关数据绘制如下不完整统计图表如下,请解答问题:
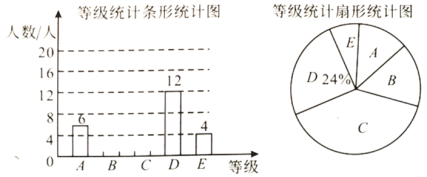
(1)该班参与测试的人数为________;
(2)![]() 等级的人数之比为
等级的人数之比为![]() ,依据数据补全统计图;
,依据数据补全统计图;
(3)扇形图中,![]() 等级人数所对应的扇形图中的圆心角为________;
等级人数所对应的扇形图中的圆心角为________;
(4)若全年级共有1400人,请估计年级部测试等级在![]() 等级以上(包括
等级以上(包括![]() 级)的学生人数.
级)的学生人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形![]() 中,
中,![]() ,点
,点![]() 是对角线
是对角线![]() 上一点,连接
上一点,连接![]() ,过点
,过点![]() 作
作![]() ,交
,交![]() 于点
于点![]() ,连接
,连接![]() ,交
,交![]() 于点
于点![]() ,将
,将![]() 沿
沿![]() 翻折,得到
翻折,得到![]() ,连接
,连接![]() ,交
,交![]() 于点
于点![]() ,若点
,若点![]() 是
是![]() 的中点,则
的中点,则![]() 的周长是( )
的周长是( )
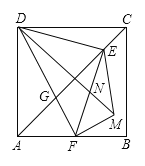
A.![]() B.
B.![]()
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
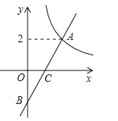
【题目】如图,平面直角坐标系xOy中,一次函数y=kx-k的图象与函数y=![]() (x>0)的图象交点为A,与y轴交于点B,P是x轴上一点,且△PAB的面积是4,则P的坐标____.
(x>0)的图象交点为A,与y轴交于点B,P是x轴上一点,且△PAB的面积是4,则P的坐标____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC的内切圆⊙O与BC、CA、AB分别相切于点D、E、F,且AB=5,BC=13,CA=12,则阴影部分(即四边形AEOF)的面积是( )
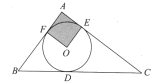
A.4B.6.25C.7.5D.9
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在矩形ABCD中,AB=6,BC=8,点E是边CD上的点,且CE=4,过点E作CD的垂线,并在垂线上截取EF=3,连接CF.将△CEF绕点C按顺时针方向旋转,记旋转角为a.
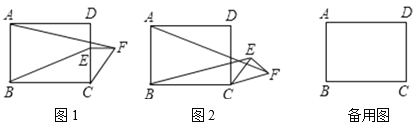
(1)问题发现
当a=0°时,AF= ,BE= ,![]() = ;
= ;
(2)拓展探究
试判断:当0°≤a°<360°时,![]() 的大小有无变化?请仅就图2的情况给出证明.
的大小有无变化?请仅就图2的情况给出证明.
(3)问题解决
当△CEF旋转至A,E,F三点共线时,直接写出线段BE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】菱形ABCD中,∠ABC=30°,AC⊥BD,点E在对角线BD上,∠AED=45°,P是菱形上一点,若△AEP是以AE为直角边为直角三角形,则tan∠APE的值为________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com