
°æƒø°ø±±æ©∫Õ…œ∫£∂º”–ºÏ≤‚–¬π⁄∑Œ—◊≤°∂浃“«∆˜ø…π©Õ‚µÿ π”√£¨∆‰÷–±±æ©”–![]() …œ∫£”–
…œ∫£”–![]() î£Æ
î£Æ
£®1£©“—÷™Œ‰∫∫–Ë“™![]() Œ¬÷›–Ë“™
Œ¬÷›–Ë“™![]() ¥”±±æ©°¢…œ∫£Ω´“«∆˜‘ÀÕ˘Œ‰∫∫°¢Œ¬÷›µƒ∑—”√»Áœ¬±ÌÀ˘ 棨”–πÿ≤ø√≈º∆ªÆ”√
¥”±±æ©°¢…œ∫£Ω´“«∆˜‘ÀÕ˘Œ‰∫∫°¢Œ¬÷›µƒ∑—”√»Áœ¬±ÌÀ˘ 棨”–πÿ≤ø√≈º∆ªÆ”√![]() ‘™‘ÀÀÕ’‚–©“«∆˜£Æ«Îƒ„…˺∆“ª÷÷‘ÀÀÕ∑Ω∞∏£¨ πŒ‰∫∫°¢Œ¬÷›ƒ‹µ√µΩÀ˘–Ë“«∆˜£¨∂¯«“‘À∑—’˝∫√πª”√£Æ
‘™‘ÀÀÕ’‚–©“«∆˜£Æ«Îƒ„…˺∆“ª÷÷‘ÀÀÕ∑Ω∞∏£¨ πŒ‰∫∫°¢Œ¬÷›ƒ‹µ√µΩÀ˘–Ë“«∆˜£¨∂¯«“‘À∑—’˝∫√πª”√£Æ
£®2£©Œ™¡ÀΩ⁄‘º‘ÀÀÕ◊ Ω£¨÷–—Î∑¿øÿπ§◊˜◊ÈÕ≥“ªµ˜≈‰“«∆˜£¨∑÷≈‰µΩŒ¬÷›µƒ“«∆˜≤ªƒ‹≥¨π˝![]() ‘Ú»Á∫Œµ˜≈‰£ø
‘Ú»Á∫Œµ˜≈‰£ø
÷’µ„ ∆µ„ | Œ¬÷› | Œ‰∫∫ |
±±æ© |
|
|
…œ∫£ |
|
|
°æ¥∞∏°ø£®1£©¥”±±æ©‘ÀÕ˘Œ¬÷›4‘ÀÕ˘Œ‰∫∫6¥”…œ∫£‘ÀÕ˘Œ¬÷›2‘ÀÕ˘Œ‰∫∫2£®2£©¥”…œ∫£≈‰ÀÕ4îµΩŒ¬÷›£¨¥”±±æ©≈‰ÀÕ1îµΩŒ¬÷›£¨Œ‰∫∫9î
°æΩ‚Œˆ°ø
£®1£©…˱±æ©‘ÀÕ˘Œ¬÷›x‘Ú…œ∫£‘ÀÕ˘Œ¬÷›y”…“‚µ√µ»¡øπÿœµ¡–≥ˆ∑Ω≥Ã◊È£¨Ω‚∑Ω≥Ã◊Ⱥ¥ø…£Æ
£®2£©Ω·∫œ±Ì∏Òµƒ ˝æ›£¨º¥ø…µ√µΩ‘ÀÀÕ◊ Ω◊ÓµÕµƒ∑Ω∞∏£Æ
Ω‚£∫£®1£©Ω‚£∫…Ë¥”±±æ©‘ÀÕ˘Œ¬÷›x¥”…œ∫£‘ÀÕ˘Œ¬÷›yî£Æ
“¿Ã‚“‚£¨µ√![]()
Ω‚µ√![]()
¥”±±æ©‘ÀÕ˘Œ‰∫∫£∫10-x=10-4=6£®Ã®£©£ª
¥”…œ∫£‘ÀÕ˘Œ‰∫∫£∫4-y=4-2=2£®Ã®£©£ª
¥£∫¥”±±æ©‘ÀÕ˘Œ¬÷›4‘ÀÕ˘Œ‰∫∫6¥”…œ∫£‘ÀÕ˘Œ¬÷›2‘ÀÕ˘Œ‰∫∫2î£Æ
£®2£©”…±Ì∏Ò÷–µƒ ˝æ›ø…µ√≥ˆ£¨…œ∫£‘ÀÀÕµΩŒ¬÷›µƒ∑—”√◊ÓµÕ£¨∆‰¥Œ «±±æ©‘ÀÀÕµΩŒ¬÷›µƒ∑—”√£¨«“∑÷≈‰µΩŒ¬÷›µƒ“«∆˜≤ªƒ‹≥¨π˝5
°‡Œ™¡ÀΩ⁄‘º◊ Ω£¨¥”…œ∫£≈‰ÀÕ4îµΩŒ¬÷›£¨¥”±±æ©≈‰ÀÕ1îµΩŒ¬÷›£¨Œ‰∫∫9î£Æ


 ∫ËÕºÕº È∫ƺŸ◊˜“µºŸ∆⁄◊˜“µº™¡÷¥Û—ß≥ˆ∞Ê…Áœµ¡–¥∞∏
∫ËÕºÕº È∫ƺŸ◊˜“µºŸ∆⁄◊˜“µº™¡÷¥Û—ß≥ˆ∞Ê…Áœµ¡–¥∞∏
| ƒÍº∂ | ∏fl÷–øŒ≥à | ƒÍº∂ | ≥ı÷–øŒ≥à |
| ∏fl“ª | ∏fl“ª√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı“ª | ≥ı“ª√‚∑—øŒ≥ÃÕ∆ºˆ£° |
| ∏fl∂˛ | ∏fl∂˛√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı∂˛ | ≥ı∂˛√‚∑—øŒ≥ÃÕ∆ºˆ£° |
| ∏fl»˝ | ∏fl»˝√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı»˝ | ≥ı»˝√‚∑—øŒ≥ÃÕ∆ºˆ£° |
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø»ÁÕº£¨“—÷™![]() £¨“‘
£¨“‘![]() Œ™÷±æ∂µƒ
Œ™÷±æ∂µƒ![]() Ωª±fl
Ωª±fl![]() ”⁄µ„
”⁄µ„![]() £¨
£¨![]() ”Î
”Î![]() œ‡«–£Æ
œ‡«–£Æ
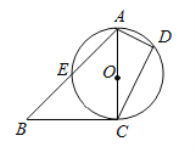
£®1£©»Ù![]() £¨«Û÷§£∫
£¨«Û÷§£∫![]() £ª
£ª
£®2£©µ„![]() «
«![]() …œ“ªµ„£¨«“
…œ“ªµ„£¨«“![]() £¨
£¨![]() ¡Ωµ„‘⁄
¡Ωµ„‘⁄![]() µƒ“Ï≤‡£Æ»Ù
µƒ“Ï≤‡£Æ»Ù![]() £¨
£¨![]() £¨
£¨![]() £¨«Û
£¨«Û![]() µƒ√ʪ˝£Æ
µƒ√ʪ˝£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
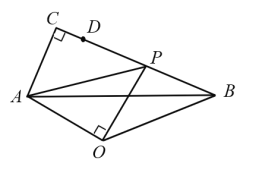
°æƒø°ø»ÁÕº£¨![]() ÷–£¨
÷–£¨![]() µ„
µ„![]() «
«![]() ±fl…œ“ªµ„£¨
±fl…œ“ªµ„£¨![]() µ„
µ„![]() «œfl∂Œ
«œfl∂Œ![]() …œµƒ∂ص„£¨¡¨Ω”
…œµƒ∂ص„£¨¡¨Ω”![]() £¨“‘
£¨“‘![]() Œ™–±±fl‘⁄
Œ™–±±fl‘⁄![]() µƒœ¬∑Ω◊˜µ»—¸
µƒœ¬∑Ω◊˜µ»—¸![]() ¡¨Ω”
¡¨Ω”![]() µ±
µ±![]() ¥”µ„
¥”µ„![]() ≥ˆ∑¢‘À∂Ø÷¡µ„
≥ˆ∑¢‘À∂Ø÷¡µ„![]() Õ£÷πµƒπ˝≥Ã÷–£¨
Õ£÷πµƒπ˝≥Ã÷–£¨![]() √ʪ˝µƒ◊Ó¥Û÷µµ»”⁄_____________________
√ʪ˝µƒ◊Ó¥Û÷µµ»”⁄_____________________![]()
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
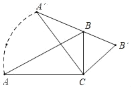
°æƒø°ø»ÁÕº£¨‘⁄Rt°˜ABC÷–£¨°œACB£Ω90°„£¨°œA£Ω30°„£¨AB£Ω6£¨Ω´Rt°˜ABC»∆µ„CÀ≥ ±’Ζ˝◊™£¨ π–±±flA°‰B°‰π˝Bµ„£¨‘Úœfl∂ŒCA…®π˝µƒ√ʪ˝Œ™_____£Æ£®Ω·π˚±£¡Ù∏˘∫≈∫Õ¶–£©
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø»ÁÕº1£¨‘⁄æÿ–Œ÷Ω∆¨![]() ÷–£¨
÷–£¨![]() £¨
£¨![]() £¨’€µ˛÷Ω∆¨ π
£¨’€µ˛÷Ω∆¨ π![]() µ„¬‰‘⁄±fl
µ„¬‰‘⁄±fl![]() …œµƒ
…œµƒ![]() ¥¶£¨≤∫€Œ™
¥¶£¨≤∫€Œ™![]() £Æπ˝µ„
£Æπ˝µ„![]() ◊˜
◊˜![]() Ωª
Ωª![]() ”⁄
”⁄![]() £¨¡¨Ω”
£¨¡¨Ω”![]() £Æ
£Æ
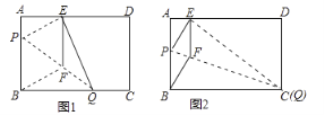
£®1£©«Û÷§£∫Àƒ±fl–Œ![]() Œ™¡‚–Œ£ª
Œ™¡‚–Œ£ª
£®2£©µ±µ„![]() ‘⁄
‘⁄![]() ±fl…œ“∆∂Ø ±£¨’€∫€µƒ∂Àµ„
±fl…œ“∆∂Ø ±£¨’€∫€µƒ∂Àµ„![]() °¢
°¢![]() “≤ÀÊ÷Æ“∆∂Ø£ª
“≤ÀÊ÷Æ“∆∂Ø£ª
¢Ÿµ±µ„![]() ”ε„
”ε„![]() ÷ÿ∫œ ±£®»ÁÕº2£©£¨«Û¡‚–Œ
÷ÿ∫œ ±£®»ÁÕº2£©£¨«Û¡‚–Œ![]() µƒ±fl≥§£ª
µƒ±fl≥§£ª
¢⁄»Ùœfi∂®![]() °¢
°¢![]() ∑÷±‘⁄±fl
∑÷±‘⁄±fl![]() °¢
°¢![]() …œ“∆∂Ø£¨«Û
…œ“∆∂Ø£¨«Û![]() µƒƒ⁄«–‘≤∞Îæ∂µƒ»°÷µ∑∂Œß£Æ
µƒƒ⁄«–‘≤∞Îæ∂µƒ»°÷µ∑∂Œß£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø»ÁÕº£¨∫Ø ˝![]() £®
£®![]() £¨
£¨![]() £¨
£¨![]() Œ™≥£ ˝£¨«“
Œ™≥£ ˝£¨«“![]() £©æ≠π˝µ„
£©æ≠π˝µ„![]() °¢
°¢![]() £¨«“
£¨«“![]() £¨œ¬¡–Ω·¬€£∫
£¨œ¬¡–Ω·¬€£∫
¢Ÿ![]() £ª¢⁄
£ª¢⁄![]() £ª¢€»Ùµ„
£ª¢€»Ùµ„![]() £¨
£¨![]() ‘⁄≈◊ŒÔœfl…œ£¨‘Ú
‘⁄≈◊ŒÔœfl…œ£¨‘Ú![]() £ª¢‹
£ª¢‹![]() .∆‰÷–Ω·¬€’˝»∑µƒ”–£® £©∏ˆ
.∆‰÷–Ω·¬€’˝»∑µƒ”–£® £©∏ˆ
A.1B.2C.3D.4
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
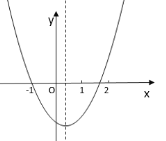
°æƒø°ø∂˛¥Œ∫Ø ˝y£Ωax2+bx+c£®a°Ÿ0£©µƒÕºœÛ»ÁÕºÀ˘ 棨œ¬¡–Ω·¬€£∫¢Ÿb2©Å4ac£æ0£ª¢⁄abc£º0£ª¢€4a+b£Ω0£ª¢‹4a©Å2b+c£æ0£Æ∆‰÷–’˝»∑Ω·¬€µƒ∏ˆ ˝ «£®°°°°£©
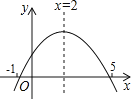
A.4B.3C.2D.1
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
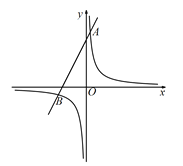
°æƒø°ø»ÁÕº£¨‘⁄∆Ω√Êœµ÷–£¨“ª¥Œ∫Ø ˝![]() µƒÕºœÒæ≠π˝∂®µ„A£¨∑¥±»¿˝∫Ø ˝
µƒÕºœÒæ≠π˝∂®µ„A£¨∑¥±»¿˝∫Ø ˝![]() µƒÕºœÒæ≠π˝µ„A£¨«“”Γª¥Œ∫Ø ˝
µƒÕºœÒæ≠π˝µ„A£¨«“”Γª¥Œ∫Ø ˝![]() µƒÕºœÒœ‡Ωª”⁄µ„B£®
µƒÕºœÒœ‡Ωª”⁄µ„B£®![]() £¨m£©£Æ
£¨m£©£Æ
£®1£©«Ûm°¢aµƒ÷µ£ª
£®2£©…Ë∫·◊¯±ÍŒ™nµƒµ„P‘⁄∑¥±»¿˝∫Ø ˝ÕºœÛµƒµ⁄»˝œÛœfi…œ£¨«“‘⁄µ„B”“≤‡£¨¡¨Ω”AP°¢BP£¨°˜ABPµƒ√ʪ˝Œ™12£¨«Û¥˙ ˝ Ω![]() µƒ÷µ£Æ
µƒ÷µ£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø£®∏≈ƒÓ»œ ∂£©
»Ù“‘‘≤µƒ÷±æ∂µƒ¡Ω∏ˆ∂Àµ„∫Õ‘≤Õ‚“ªµ„Œ™∂•µ„µƒ»˝Ω«–Œ «µ»—¸»˝Ω«–Œ£¨‘Ú‘≤Õ‚’‚“ªµ„≥∆Œ™’‚∏ˆ‘≤µƒæ∂µ»µ„£Æ
£® ˝—ß¿ÌΩ‚£©
£®1£©»ÁÕº¢Ÿ£¨AB «°—Oµƒ÷±æ∂£¨µ„PŒ™°—OÕ‚“ªµ„£¨¡¨Ω”APΩª°—O”⁄µ„C£¨PC£ΩAC£Æ
«Û÷§£∫µ„PŒ™°—Oµƒæ∂µ»µ„£Æ

£®2£©“—÷™AB «°—Oµƒ÷±æ∂£¨µ„PŒ™°—Oµƒæ∂µ»µ„£¨¡¨Ω”APΩª°—O”⁄µ„C£¨»ÙPC£Ω2AC£Æ«Û![]() µƒ÷µ£Æ
µƒ÷µ£Æ
£®Œ Ã‚Ω‚æˆ£©
£®3£©»ÁÕº¢⁄£¨“—÷™AB «°—Oµƒ÷±æ∂£Æ»Ùµ„PŒ™°—Oµƒæ∂µ»µ„£¨¡¨Ω”APΩª°—O”⁄µ„C£¨PC£Ω3AC£Æ¿˚”√÷±≥fl∫Õ‘≤πÊ◊˜≥ˆÀ˘”–¬˙◊„Ãıº˛µƒµ„P£Æ£®±£¡Ù◊˜Õº∫€º££¨≤ª–¥◊˜∑®£©

≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
π˙º —ß–£”≈—° - ¡∑œ∞≤·¡–±Ì - ‘¡–±Ì
∫˛±± °ª•¡™Õ¯Œ•∑®∫Õ≤ª¡º–≈œ¢æŸ±®∆Ωî | Õ¯…œ”–∫¶–≈œ¢æŸ±®◊®«¯ | µÁ–≈’©∆≠柱®◊®«¯ | …Ê¿˙ ∑–ÈŒfi÷˜“”–∫¶–≈œ¢æŸ±®◊®«¯ | …Ê∆Û«÷»®æŸ±®◊®«¯
Œ•∑®∫Õ≤ª¡º–≈œ¢æŸ±®µÁª∞£∫027-86699610 柱®” œ‰£∫58377363@163.com