
【题目】如图,已知![]() ,以
,以![]() 为直径的
为直径的![]() 交边
交边![]() 于点
于点![]() ,
,![]() 与
与![]() 相切.
相切.
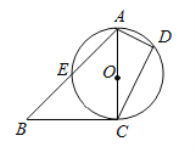
(1)若![]() ,求证:
,求证:![]() ;
;
(2)点![]() 是
是![]() 上一点,且
上一点,且![]() ,
,![]() 两点在
两点在![]() 的异侧.若
的异侧.若![]() ,
,![]() ,
,![]() ,求
,求![]() 的面积.
的面积.
【答案】(1)见解析;(2)![]()
【解析】
(1)连接CE,依据题意和圆周角定理求得△ABC是等腰直角三角形,然后根据圆周角定理和等腰三角形三线合一的性质求解即可;
(2)连接![]() ,并延长
,并延长![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() ,
,![]() ,根据圆周角定理结合已知条件可得
,根据圆周角定理结合已知条件可得![]() ,从而判定
,从而判定![]() ,得到
,得到![]() ,从而根据垂径定理可得EH=CH,根据三角形中位线定理可求
,从而根据垂径定理可得EH=CH,根据三角形中位线定理可求![]() ,然后设圆的半径为r,根据勾股定理列方程即可求出r,从而求出EH,然后根据相似三角形的判定及性质求出AB,再根据平行线的距离处处相等可得
,然后设圆的半径为r,根据勾股定理列方程即可求出r,从而求出EH,然后根据相似三角形的判定及性质求出AB,再根据平行线的距离处处相等可得![]() ,从而求出结论.
,从而求出结论.
(1)证明:连接![]() .
.
![]() 为
为![]() 的直径,
的直径,![]() 与
与![]() 相切,
相切,
![]() ,
,
![]() ,
,
![]() ,
,
∴△ABC是等腰直角三角形,
![]() ,
,
![]() .
.
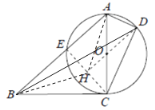
(2)连接![]() ,并延长
,并延长![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() ,
,![]() .
.
![]() ,
,![]() ,
,
![]() ,
,
![]() .
.
![]() 为直径,
为直径,
![]() ,
,
![]() ,
,
![]() 为
为![]() 中点.
中点.
![]() ,
,
![]()
设![]() 的半径为
的半径为![]()
在![]() 中,
中,![]() ,
,
在![]() 中,
中,![]() ,
,
![]()
解得![]() 或
或![]() (舍去)
(舍去)
![]() ,
,
由勾股定理得![]()
![]() .
.
![]() ,
,![]() ,
,
![]() .
.
![]()
解得![]() .
.
![]() ,
,
![]()


科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,已知抛物线![]() 与x轴交于A(-1,0),B(3,0)两点,与y轴交于点C.
与x轴交于A(-1,0),B(3,0)两点,与y轴交于点C.
(1)求该抛物线的解析式;
(2)如图①,若点D是抛物线上一动点,设点D的横坐标为m(0<m<3),连接CD,BD,BC,AC,当△BCD的面积等于△AOC面积的2倍时,求m的值;
(3)若点N为抛物线对称轴上一点,请在图②中探究抛物线上是否存在点M,使得以B,C,M,N为顶点的四边形是平行四边形?若存在,请直接写出所有满足条件的点M的坐标;若不存在,请说明理由.


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,直线![]() 与
与![]() 轴交于点
轴交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,点
,点![]() 为线段
为线段![]() 的中点,将直线
的中点,将直线![]() 向右平移
向右平移![]() 个单位长度,
个单位长度,![]() 、
、![]() 、
、![]() 的对应点为
的对应点为![]() 、
、![]() 、
、![]() ,反比例函数
,反比例函数![]() 的图象经过点
的图象经过点![]() ,连接
,连接![]() 、
、![]() .
.
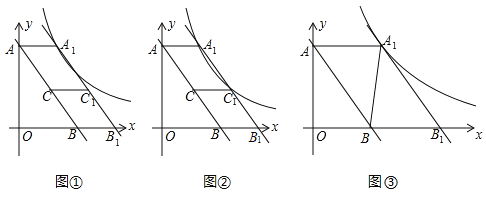
(1)当![]() 时,求
时,求![]() 的值;
的值;
(2)如图②, 当反比例函数的图象经过点![]() 时, 求四边形
时, 求四边形![]() 的面积;
的面积;
(3)如图③,连接![]() ,当
,当![]() 为等腰三角形时,求
为等腰三角形时,求![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】实验探究:
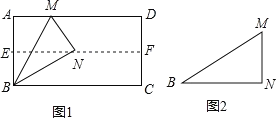
(1)如图1,对折矩形纸片ABCD,使AD与BC重合,得到折痕EF,把纸片展开;再一次折叠纸片,使点A落在EF上,并使折痕经过点B,得到折痕BM,同时得到线段BN,MN.请你观察图1,猜想∠MBN的度数是多少,并证明你的结论.
(2)将图1中的三角形纸片BMN剪下,如图2,折叠该纸片,探究MN与BM的数量关系,写出折叠方案,并结合方案证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,点![]() ,点
,点![]() .将
.将![]() 绕点
绕点![]() 顺时针旋转,得
顺时针旋转,得![]() ,点
,点![]() ,
,![]() 旋转后的对应点为
旋转后的对应点为![]() ,
,![]() .记旋转角为
.记旋转角为![]() .
.
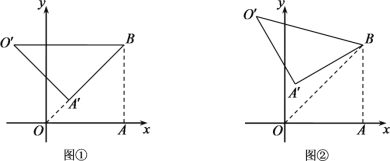
(1)如图①,当![]() 时,求点
时,求点![]() 的坐标;
的坐标;
(2)如图②,当![]() 时,求点
时,求点![]() 的坐标;
的坐标;
(3)连接![]() ,设线段
,设线段![]() 的中点为
的中点为![]() ,连接
,连接![]() ,求线段
,求线段![]() 的长的最小值(直接写出结果即可).
的长的最小值(直接写出结果即可).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为庆祝![]() 年中国航天日,发扬中国航天精神,激发青少年崇尚科学探索未知和敢于创新的热情,某校举行班级歌咏比赛,歌曲有:《祖国不会忘记》,《飞天》,《仰望星空》(分别用字母
年中国航天日,发扬中国航天精神,激发青少年崇尚科学探索未知和敢于创新的热情,某校举行班级歌咏比赛,歌曲有:《祖国不会忘记》,《飞天》,《仰望星空》(分别用字母![]() ,
,![]() ,
,![]() 依次表示这三首歌曲).比赛时,将
依次表示这三首歌曲).比赛时,将![]() ,
,![]() ,
,![]() 这三个字母分别写在
这三个字母分别写在![]() 张无差别不透明的卡片正面上,洗匀后正面向下放在桌面上,九(1)班班长先从中随机抽取一张卡片放回后洗匀,再由九(2)班班长从中随机抽取一张卡片,进行歌咏比赛.
张无差别不透明的卡片正面上,洗匀后正面向下放在桌面上,九(1)班班长先从中随机抽取一张卡片放回后洗匀,再由九(2)班班长从中随机抽取一张卡片,进行歌咏比赛.
(1)九(1)班抽中歌曲《祖国不会忘记》的概率是______;
(2)试用画树状图或列表的方法表示所有可能的结果,并求出九(1)班和九(2)班抽中不同歌曲的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
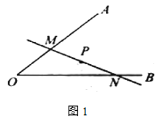
【题目】定义:如图1,已知锐角![]() 内有定点
内有定点![]() ,过点
,过点![]() 任意作一条直线
任意作一条直线![]() ,分别交射线
,分别交射线![]() ,
,![]() 于点M,N.若
于点M,N.若![]() 是线段
是线段![]() 的中点时,则称直线
的中点时,则称直线![]() 是
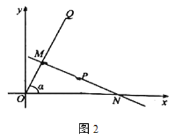
是![]() 的中点直线.如图2,射线
的中点直线.如图2,射线![]() 的解析式为
的解析式为![]() 与
与![]() 轴的夹角为
轴的夹角为![]() ,
,![]() ,
,![]() 为
为![]() 的中点直线.
的中点直线.
(1)求直线![]() 的解析式;
的解析式;
(2)若过点![]() 任意作一条直线
任意作一条直线![]() ,分别交射线
,分别交射线![]() ,
,![]() 轴的正半轴于点
轴的正半轴于点![]() ,
,![]() ,记
,记![]() 的面积为
的面积为![]() ,
,![]() 的面积为
的面积为![]() .求证:
.求证:![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】绘制函数![]() 的图象,我们经历了如下过程:确定自变量
的图象,我们经历了如下过程:确定自变量![]() 的取值范围是
的取值范围是![]() ;列表-描点--连线,得到该函数的图象如图所示
;列表-描点--连线,得到该函数的图象如图所示
| ... |
|
|
|
|
|
|
|
|
|
|
|
|
|
| ... |
| ... |
|
|
|
|
|
|
|
|
|
|
|
|
|
| ... |
观察函数图象,回答下列问题:
(1)函数图象在第 象限;
(2)函数图象的对称性是
B.只是轴对称图形,不是中心对称图形
A.既是轴对称图形,又是中心对称图形
D.既不是轴对称图形,也不是中心对称图形
C.不是轴对称图形,而是中心对称图形
(3)在![]() 时,当
时,当![]() 时,函数
时,函数![]() 有最 (大,小)值,且这个最值等于
有最 (大,小)值,且这个最值等于
在![]() 时,当
时,当![]() 时,函数
时,函数![]() 有最 (大,小)值,且这个最值等于
有最 (大,小)值,且这个最值等于
(4)方程![]() 是否有实数解?说明
是否有实数解?说明
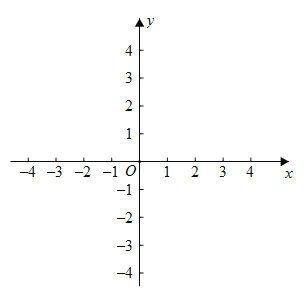
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】北京和上海都有检测新冠肺炎病毒的仪器可供外地使用,其中北京有![]() 台,上海有
台,上海有![]() 台.
台.
(1)已知武汉需要![]() 台,温州需要
台,温州需要![]() 台,从北京、上海将仪器运往武汉、温州的费用如下表所示,有关部门计划用
台,从北京、上海将仪器运往武汉、温州的费用如下表所示,有关部门计划用![]() 元运送这些仪器.请你设计一种运送方案,使武汉、温州能得到所需仪器,而且运费正好够用.
元运送这些仪器.请你设计一种运送方案,使武汉、温州能得到所需仪器,而且运费正好够用.
(2)为了节约运送资金,中央防控工作组统一调配仪器,分配到温州的仪器不能超过![]() 台,则如何调配?
台,则如何调配?
终点 起点 | 温州 | 武汉 |
北京 |
|
|
上海 |
|
|
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com